CS13002 PDS Lab, Spring 2003, Section 1/A

Assignment 8

But if you are through with Assigment 7, here is a bonus exercise for you. (Bonus means that any marks you get for this exrecise will be added to your total (after scaling, of course), but the marks for this exercise will not be added to the total credit for the lab.)

[Permutations and runs]

• Write a recursive function to generate all permutations of 1,2,...,n. Do not print the permutations, but store them in a dynamic array. The array must be allocated exactly as much memory as to store the n! permutations. For example, for the case n=3 the array may look like:

  123132213231312321
  

  where each element (of {1,...,n}) occupies a cell in the array. Thus the size of the array will be n! times n. If n is known, we do not need separator between two permutations, since the size of each permutation is exactly known.

  If you choose, you can use a two-dimensional array for storing the permutations. In that case a natural strategy is to store a permutation in each row and have n! rows to store all the permutations. For n=3 the 2-D array would look like:

  123
  132
  231
  213
  312
  321
  

• A run in a permutation is a maximal monotonic increasing sequence of adjacent elements in the permutation. For example, the runs in

  257183496
  

  are

  257, 18, 349, 6.
  

  Note that every run (except the last) is followed by a descent (also called a fall). For example, in the above permutation the descents are 71, 83 and 96. It is clear that if a permutation has k+1 runs, then it has exactly k descents, and conversely. Let us denote by the notation

  <n,k>
  

  the number of permutations of 1,...,n with exactly k descents. The numbers <n,k> are called Eulerian numbers. The following table shows all the permutations of 1,2,3,4 and the runs and descents in each permutation. This list gives us the values of <4,k>.
  

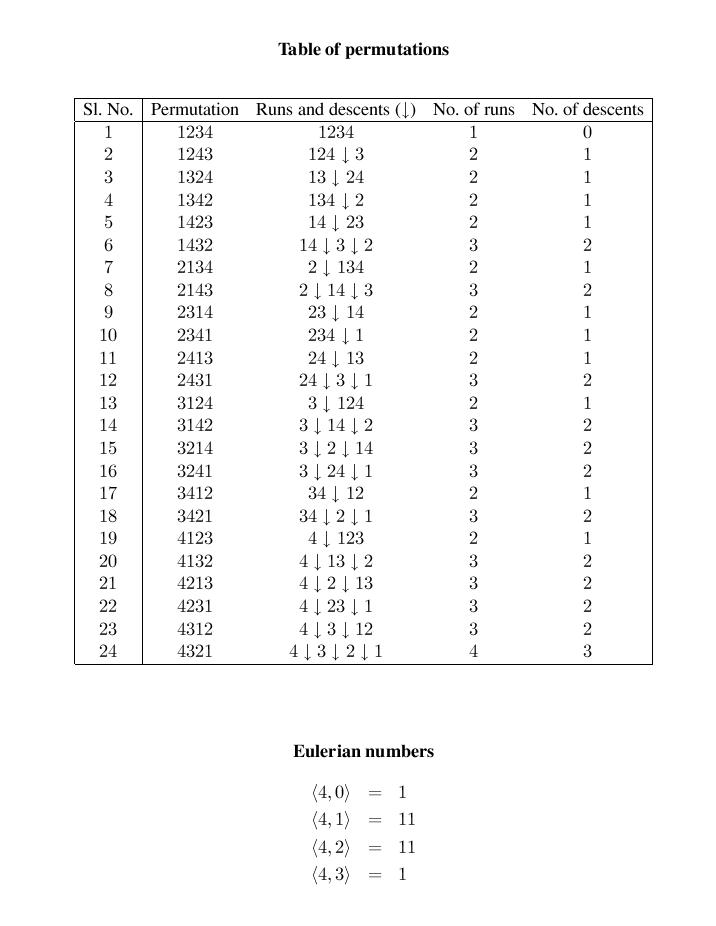
  Use the list of all permutations obtained from the previous step to enumerate <n,k> for n=1,...,8 and k=0,1,...,n-1.

• It is known that the Eulerian numbers satisfy the following recurrence relation:

  <n,0> = 1.
  <n,k> = 0, if k >= n.
  <n.k> = (k+1)<n-1,k> + (n-k)<n-1,k-1>, otherwise.
  

  Write a recursive function to compute <n,k> for n=1,...,8 and k=0,1,...,n-1.

• Finally avoid recursion and write an iterative function to compute <n,k> for n=1,...,8 and k=0,1,...,n-1. Use a 2-dimensional dynamic array. The array must be allocated exactly the amount of memory needed for the above computation.

  
  Format of output

                      k = 0  k = 1  k = 2  k = 3  k = 4  k = 5  k = 6  k = 7
  n = 1  Enumerative      x
         Recursive        x
         Iterative        x
  n = 2  Enumerative      x      x
         Recursive        x      x
         Iterative        x      x
  n = 3  Enumerative      x      x      x
         Recursive        x      x      x
         Iterative        x      x      x
  n = 4  Enumerative      x     xx     xx      x
         Recursive        x     xx     xx      x
         Iterative        x     xx     xx      x
  n = 5  Enumerative      x     xx     xx     xx      x
         Recursive        x     xx     xx     xx      x
         Iterative        x     xx     xx     xx      x
  n = 6  Enumerative      x     xx    xxx    xxx     xx      x
         Recursive        x     xx    xxx    xxx     xx      x
         Iterative        x     xx    xxx    xxx     xx      x
  n = 7  Enumerative      x    xxx   xxxx   xxxx   xxxx    xxx      x
         Recursive        x    xxx   xxxx   xxxx   xxxx    xxx      x
         Iterative        x    xxx   xxxx   xxxx   xxxx    xxx      x
  n = 8  Enumerative      x    xxx   xxxx  xxxxx  xxxxx   xxxx    xxx      x
         Recursive        x    xxx   xxxx  xxxxx  xxxxx   xxxx    xxx      x
         Iterative        x    xxx   xxxx  xxxxx  xxxxx   xxxx    xxx      x
  

Best of luck for the EndSem. And also for all programming endeavors that you will undertake in future. We hope that these practice sessions will prove to be useful!!!

[Course home] [Home]