CS13002 PDS Lab, Spring 2003, Section 1/A, Assignment 7

CS13002 PDS Lab, Spring 2003, Section 1/A

Assignment 7

[Trees]

A tree consists of nodes (also called vertices, represented by circles with a label) and edges (also called links, represented by line segments joining pairs of different nodes) with a distinguished node known as the root. A tree is defined recursively as follows:

A single node (and nothing else) is a tree. The only node in the tree is the root of the tree.
Let T₁,...,T_n be trees with respective roots a₁,...,a_n. Then a tree with root a is obtained by creating a new node (with label a) and joining a to a_i for all i=1,...,n. In this case a₁,...,a_n are called the children of a. This recursive step is described in the figure below.

An example of a tree is given below:

In this tree the root is a. It has four children b, c, d and e. The node b has no children, whereas c has three children: f, g and h, and so on. A node in a tree having no children is called a leaf. In the example above the leaves are b, f, g, k, l, i and j.

A binary tree is a tree in which every node has at most two children, commonly called the left child and the right child. Structures and pointers can be used to represent a node of a binary tree:

#define MAXLEN 100
struct node {
   char label[MAXLEN];
   struct node *L;
   struct node *R;
};

Thus a node `looks like' as shown in the following figure. The arrowed lines represent pointers to nodes.

If a node does not have a left child, its L pointer should be NULL. Similarly absence of the right child is represented by a NULL R pointer.

In this exercise you are asked to implement a representation of a (general) tree using a binary tree. In this representation the left pointer L means `the first (leftmost) child' and the right pointer R means `the next sibling (brother/sister)'. For example, consider the tree of the above figure. First consider the root a. Its first child is b, so its L pointer points to the node with label b. a has no (next) sibling, so its R pointer is NULL. b has no children, so its L pointer is NULL, whereas the next sibling of b is c. So the R pointer of b points to the node c. The first child of c is f and the next sibling of c is d. Thus the L and R pointers of c point respectively to the nodes f and d. And so on. The representation of the above tree by a binary tree under this scheme is depicted in the figure below. For the sake of convenience the original tree is also shown below.

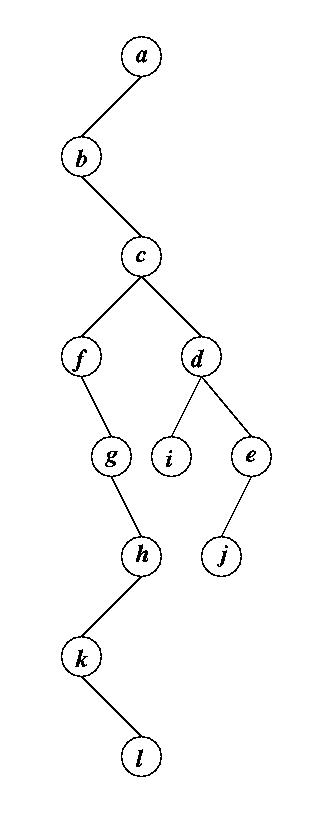
Write a program that interactively reads from the terminal the labels of the nodes and the information about the children of the nodes, builds the equivalent binary tree, prints a description of the binary tree and also a retrieved description of the original tree. For the tree shown above the input/output session should be as follows:

Label of root : a
Number of children of a : 4
Enter the label of child 1 of a : b
Enter the label of child 2 of a : c
Enter the label of child 3 of a : d
Enter the label of child 4 of a : e
Number of children of b : 0
Number of children of c : 3
Enter the label of child 1 of c : f
Enter the label of child 2 of c : g
Enter the label of child 3 of c : h
Number of children of f : 0
Number of children of g : 0
Number of children of h : 2
Enter the label of child 1 of h : k
Enter the label of child 2 of h : l
Number of children of k : 0
Number of children of l : 0
Number of children of d : 1
Enter the label of child 1 of d : i
Number of children of i : 0
Number of children of e : 1
Enter the label of child 1 of e : j
Number of children of j : 0

Equivalent binary tree :
Label : a, Left child : b, Right child : NULL.
Label : b, Left child : NULL, Right child : c.
Label : c, Left child : f, Right child : d.
Label : f, Left child : NULL, Right child : g.
Label : g, Left child : NULL, Right child : h.
Label : h, Left child : k, Right child : NULL.
Label : k, Left child : NULL, Right child : l.
Label : l, Left child : NULL, Right child : NULL.
Label : d, Left child : i, Right child : e.
Label : i, Left child : NULL, Right child : NULL.
Label : e, Left child : j, Right child : NULL.
Label : j, Left child : NULL, Right child : NULL.

The original tree :
Label : a, Children : b,c,d,e.
Label : b, Children :
Label : c, Children : f,g,h.
Label : f, Children :
Label : g, Children :
Label : h, Children : k,l.
Label : k, Children :
Label : l, Children :
Label : d, Children : i.
Label : i, Children :
Label : e, Children : j.
Label : j, Children :

Submit the input/output behavior of your program on the family tree of the Mughals as summarized in the following figure:

If you know how to tackle fie I/O in C, you may use this file. In that case you must ensure that the sequence of inputs by your program is exactly the same as given in this database file. The standard printing procedure hides from you all the prompts before scanning. It is a pain to work without these prompting messages. In order to generate the output file either do copy-and-paste from the terminal or read the above database.

Representation using adjacency matrices

Trees can also be represented by adjacency matrices. Let T be a tree with n nodes v₁,...,v_n. The adjacency matrix is an nxn matrix whose ij-th entry is 1 if there is an edge from v_i to v_j (i.e, if v_j is a child of v_i). The ij-th entry is zero otherwise.

An adjacency matrix (like any other square matrix) can be represented using the following data type:

typedef struct {
   int dim;
   int **element;
} adjMatrix;

Compute and print the adjacency matrix of the Mughal family tree. Don't key in the family tree again; use the binary tree built above to create the adjacency matrix. Also use dynamic arrays to store the entries of the matrix.

Note that the adjacency matrix depends on the ordering of the vertices. You can assign a unique serial number to each node during the time of its creation (or afterwards). In view of this we add to the data type node another entry:

struct node {
   int serialNo;
   char label[MAXLEN];
   struct node *L;
   struct node *R;
};

Before printing the adjacency matrix you must also print the serial numbers assigned to the nodes.

The typical output on our example tree should be as follows:

Adjacency matrix representation :
The following node ordering is used :
  0 : a
  1 : b
  2 : c
  3 : d
  4 : e
  5 : f
  6 : g
  7 : h
  8 : k
  9 : l
 10 : i
 11 : j
The adjacency matrix with respect to this ordering is :
 0 1 1 1 1 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 1 1 1 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 1 0
 0 0 0 0 0 0 0 0 0 0 0 1
 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 1 1 0 0
 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0

[Course home] [Home]