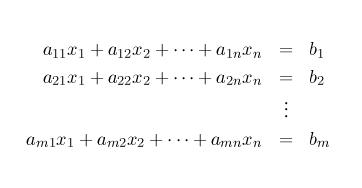
Consider a system of m linear equations in n variables:
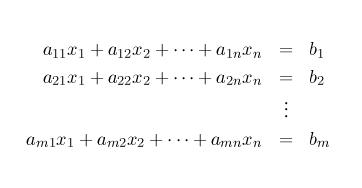
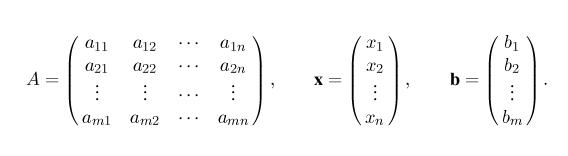
Two dimensional arrays are widely used to represent matrices. Let us plan for matrices as big as 20x20 and have a (static) two-dimensional array for storing the elements. We also need the exact number of rows and columns in a matrix.
#define MAX_DIMEN 20
typedef struct {
int rowdim; /* Number of rows */
int coldim; /* Number of columns */
float element[MAX_DIMEN][MAX_DIMEN]; /* The elements */
} matrix;
Since we are dealing with square system of equations only, we
will always have the equality of row and column dimensions in
our square matrices. In that case holding a single dimension
in the matrix structure would be sufficient. But for the sake
of generality let us allow the possibility of treatment of
mxn matrix.
A vector, on the other hand, can be represented by a one-dimensional array as follows:
typedef struct {
int dim; /* Dimension of a vector */
float element[MAX_DIMEN]; /* The elements */
} vector;
Compute the inverse A-1 of A (provided that A is non-singular, i.e., invertible). You can use the following algorithm for this computation:
By an elementary row operation on a matrix we mean one of the following operations (Note that each row corresponds to an equation.):
Start with A and another matrix B. Assume that A is an nxn matrix. B should be initialized to the nxn identity matrix I (the matrix with 1 in its main diagonal and zero elsewhere). Use a sequence of elementary row operations on A to convert it to the identity matrix. Apply the identical sequence of elementary row operations on B. When A is reduced to I, B is transformed to the inverse of A. If A can not be reduced to I, A is not invertible; report `failure' in this case.
The reduction of A to I consists of n iterative steps indexed by i=1,...,n. At the beginning of the i-th iterative step the first through (i-1)-th columns have been converted to the first i-1 columns of I. During the i-th iterative step we reduce the i-th column of A to the i-th column of I using elementary row operations. The ii-th entry of I is one. So we search for a non-zero entry among aki, k=i,...,n. If no such entry is found, report failure and terminate. If aii=0 and aki!=0 for some k>i, then interchange row i and row k. This brings a non-zero entry at the (new) ii-th location. Now divide the i-th row by the entry aii, so that we now obtain aii=1. When this is done, we make aki=0 for each k!=i by subtracting an appropriate multiple of the i-th row from the k-th one.
The following figure demonstrates a successful computation of the inverse of a matrix (Here Ri denotes the i-th row.):

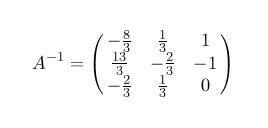

This algorithm computes A-1 in B at the end of the n-step iterative process, provided that A is invertible. On the other hand, if A is not invertible, this algorithm detects it at some stage and reports `failure'. Ask your maths teacher why this algorithm always woks as claimed.
Finally note that in C indexing of arrays starts from zero, whereas we have started numbering of equations and variables from 1. Do the relevant changes in the 1-based indexing scheme in the above description to convert it to the 0-based scheme suitable for C.
Using the value of A-1 computed as above solve the system as:
x = A-1b
Now use your solution x to compute Ax and verify that this x satisfies Ax=b (within floating point approximations).
A sample output is given below:
A : -5.00000 0.00000 -4.00000 -8.00000 9.00000 6.00000 7.00000 -7.00000 6.00000 8.00000 -10.00000 -7.00000 10.00000 9.00000 -3.00000 -5.00000 3.00000 -1.00000 10.00000 -4.00000 7.00000 -10.00000 8.00000 1.00000 2.00000 2.00000 -7.00000 5.00000 6.00000 2.00000 9.00000 -10.00000 -8.00000 -8.00000 -8.00000 -10.00000 8.00000 8.00000 -9.00000 2.00000 5.00000 10.00000 5.00000 2.00000 9.00000 10.00000 7.00000 1.00000 -2.00000 5.00000 7.00000 -6.00000 3.00000 2.00000 4.00000 -6.00000 -6.00000 5.00000 10.00000 8.00000 -3.00000 6.00000 8.00000 -1.00000 b : 9.00000 9.00000 -3.00000 4.00000 4.00000 -4.00000 -5.00000 -2.00000 Inverse of A : -0.01828 -0.26724 -0.16397 0.07274 -0.01426 0.23921 0.18380 -0.31933 0.01915 0.33907 0.16668 -0.11296 -0.05370 -0.23245 -0.19760 0.31257 -0.08421 -0.13234 -0.04793 0.05484 0.04918 0.10096 0.15943 -0.10244 -0.10606 0.05603 0.05134 0.06916 0.05217 -0.04345 -0.03610 0.09941 -0.08829 0.12891 0.12760 0.04010 0.07738 -0.07417 -0.05894 0.13431 0.01840 -0.22616 -0.16725 0.04163 0.01591 0.20245 0.14410 -0.21178 0.15023 -0.07223 -0.03655 -0.04358 -0.07914 0.05678 -0.05564 -0.05885 0.09201 0.10213 0.06998 -0.11869 -0.04355 -0.04395 -0.18903 0.10532 x : -3.08096 3.35002 -2.38514 0.03657 0.77546 -2.24474 0.48955 1.79862 Original b : 9.00000 9.00000 -3.00000 4.00000 4.00000 -4.00000 -5.00000 -2.00000 Reconstructed b : 9.00000 9.00002 -3.00000 4.00000 3.99998 -3.99999 -5.00000 -2.00001Look at the effect of floating point approximations. The reconstructed b is slightly different from the original b. These floating point errors can be reduced by a technique called pivoting. Interested students can look at books on numerical analysis to know more about this.
Remark: We recommend you to implement the following functions:
[Course home] [Home]