Show that -29 and 31 are roots of the polynomial
X3 + X2 - 905X - 2697.
What is its third root?
Show that -2931 is a root of the polynomial
X3 + 2871X2 - 174961X + 2634969.
The three roots of the polynomial
X3 + X2 - 74034X + 5294016
are integers. Find them.
The three roots of the polynomial
X3 + X2 - 28033X - 1815937
are again integers. Find them.
[The queer rope and the diligent ant] An ant is sitting at the left end of a rope of length 10 cm. At t=0 the ant starts moving along the rope to reach the other end of the rope. The ant has a speed of 1 cm per second. After every second the rope stretches instantaneously and uniformly (along its length) by 10 cm with the left end fixed at the point from where the ant started its journey. Suppose that the ant's legs provide it sufficient friction in order to withstand the stretching of the rope without slipping. Write a program to demonstrate that the ant will be able to reach the right end of the rope. Your program should also calculate how many seconds the ant would take to achieve this goal. You may assume that the length of the ant is negligible (i.e., zero).
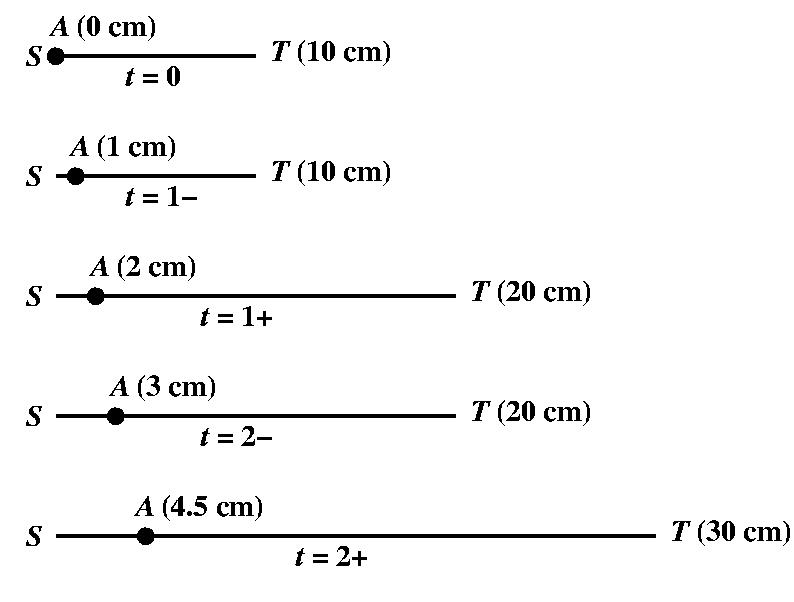
Note: Use real (float or double) arithmetic.
Note: The ant would reach the right end of the rope, even if its initial length and stretching per second were 1 km (or even a billion kilometers) instead of 10 cm. But for these dimensions the ant would take such an unbelievably large time that your program will not give you the confirmation in your life-time. Moreover, you will require more precision than what double can provide. Try solving this puzzle mathematically.