Set-reset (SR) latch

---

SR latch using NAND gates

---

SR latch using NOR gates

---

Clocked SR latch (using NAND gates)

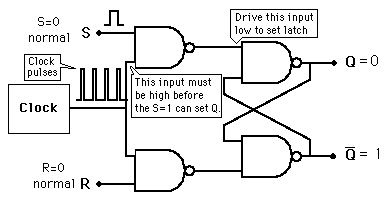Truth table Clk S R Q 1 0 0 No change 0 1 0 1 0 1 1 1 Invalid 0 No change

---

Chatterless switch

---

JK flip flop

---

Basic JK FF

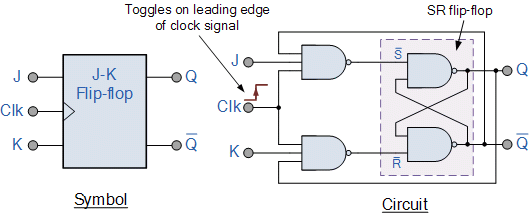Truth table Clk J K Q Q New 1 0 0 — No change 0 1 0 0 (NC) 0 1 1 0 (Q'→1) 1 0 0 1 (Q→1) 1 0 1 1 (NC) 1 1 1 0 (Q'→1) 1 1 0 1 (Q→1) 0 No change

---

Master-slave JK FF

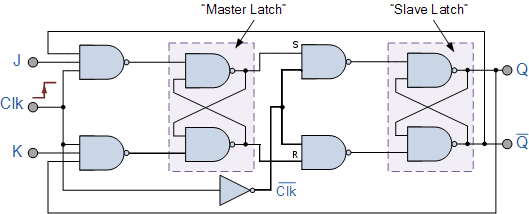	Truth table Clk J K Q Q New 0 Master: NC; MLat → SLat 1 Slave: NC 1 → 0 0 0 — MLat → SLat 0 1 — 0 (S=0, R=1) 1 0 — 1 (S=1, R=0) 1 1 1 0 (S=0, R=1) 1 1 0 1 (S=1, R=0)
Active clock edge: 1 → 0 (falling)

---

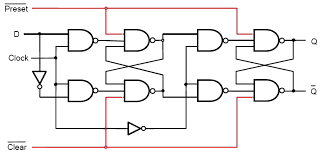
D FF with asynchronous preset and clear

---

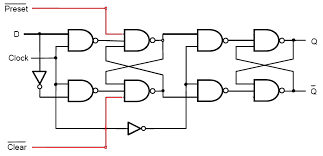
D FF with synchronous preset and clear

---

Residual problem with above DFF

1. Let the gate delay be Δ
2. Let D=0, Clk=1
3. Let D=1 and just before Δ time, Clk=0
4. Master latch has the invalid input combination of 00
5. Before valid inputs could appear at the steering gates of the master latch, Clk=0
6. Now, invalid input combination of 11 is presented to the slave steering gates, with Clock'=1
7. Slave latch has the invalid input combination of 00
8. Output of DFF is indeterminate

Problem may be avoided if D remains steady when Clk=1, allowed to change only when Clk=0

---

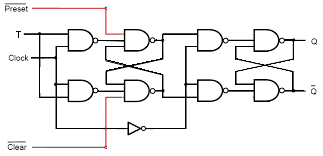
T FF with preset and clear

Similar to DFF, but J and K terminals tied (J=K=1)

---

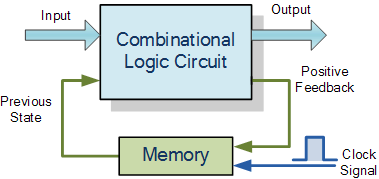
Huffman model

---

Schematic diagram

---

Setup and hold times

Setup time

It is defined as the minimum amount of time before the active clock edge by which the data must be stable for it to be latched correctly; any violation in this required time causes incorrect data to be captured and is known as a setup violation

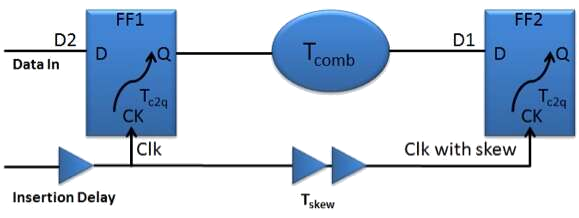
Time available for data at D2 to reach D1 after active clock edge

T_clk + T_skew - T_setup

Time needed for date to reach D1 from D2 after active clock edge

T_c2q + T_comb

Resulting constraint

T_c2q + T_comb ≤ T_clk + T_skew - T_setup

T_c2q + T_comb + T_setup ≤ T_clk + T_skew

Hold time

It is defined as the minimum amount of time after the active clock edge by which the data must be stable for it to be latched correctly; any violation in this required time causes incorrect data to be captured and is known as a hold violation

Minimum time for data at D2 to reach D1 after active clock edge

T_c2q + T_comb

Time for data to remain steady at D1 after active clock edge

T_skeq + T_hold

Resulting constraint

T_c2q + T_comb ≥ T_skeq + T_hold

---

Example for setup and hold times

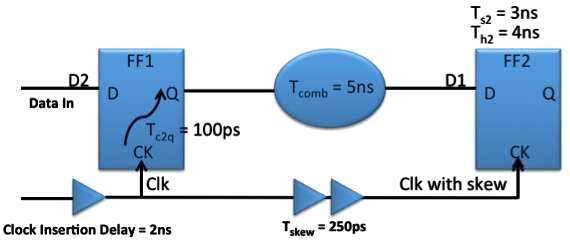
• What is the minimum clock frequency?
• T_clk + T_skew ≥ T_c2q + T_comb + T_s2
• T_clk + 0.25ns ≥ 0.1ns + 5ns + 3ns
• T_clk ≥ 7.85ns

---

Positive clock edge triggered DFF

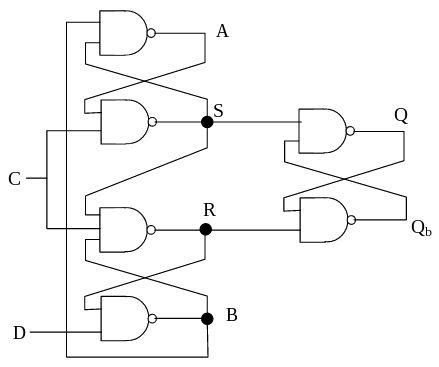
Transition table C D R S RΔ SΔ QΔ 0 — — — 1 1 Q 1 0 1 1 0 1 0 1 1 1 1 0 1 — 0 1 0 1 0 — 1 0 1 0 1 — 0 0 1 0 1

• S_Δ = (C · A)' = C'+ A'= C' + B · S = C' + (D' + R') · S
• R_Δ = ( S · C · B)' = S' + C' + B' = S' + C' + R · D
• As long as C = 0, R = S = 1 and the output latch retains its older value
• When C changes from 0 to 1, R and S change as follows:
  • If D=0: R_Δ = 0, S_Δ = 1 (from R = S = 1) and Q=0
  • If D=1: R_Δ = 1, S_Δ = 0 (from R = S = 1) and Q=1
  • Thereafter, R and S remain stable, while C=1, irrespective of changes in D
• The invalid state of R = S = 0 is never reached
• If some how R = S = 0, state immediately changes to R = 1 and S = 0

---

Types of sequential m/cs

Moore m/c

Outputs depend only on the present state

Mealy m/c

Outputs depend on the present state and also on the inputs (transducer)

Both are computationally equivalent

---

Shift register

---

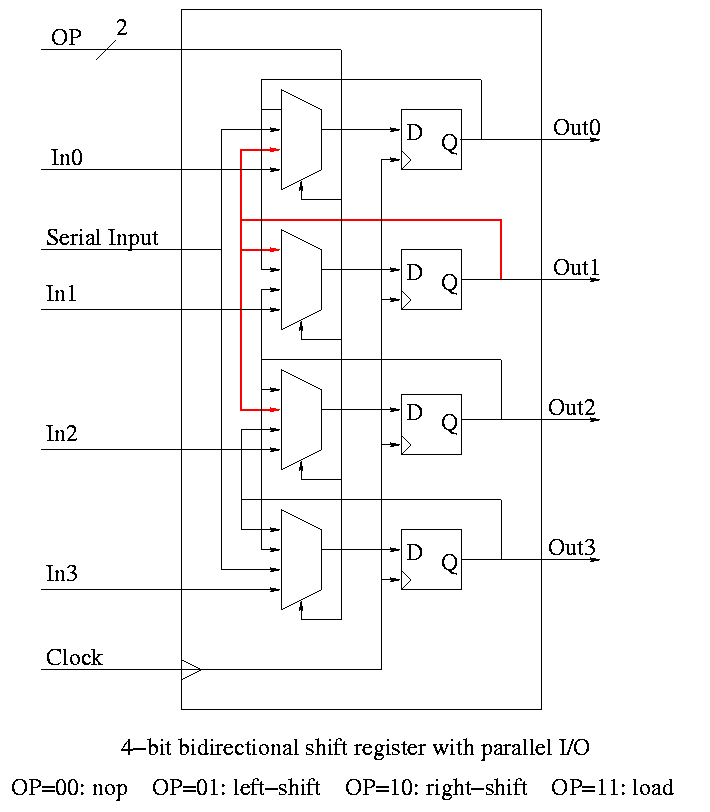
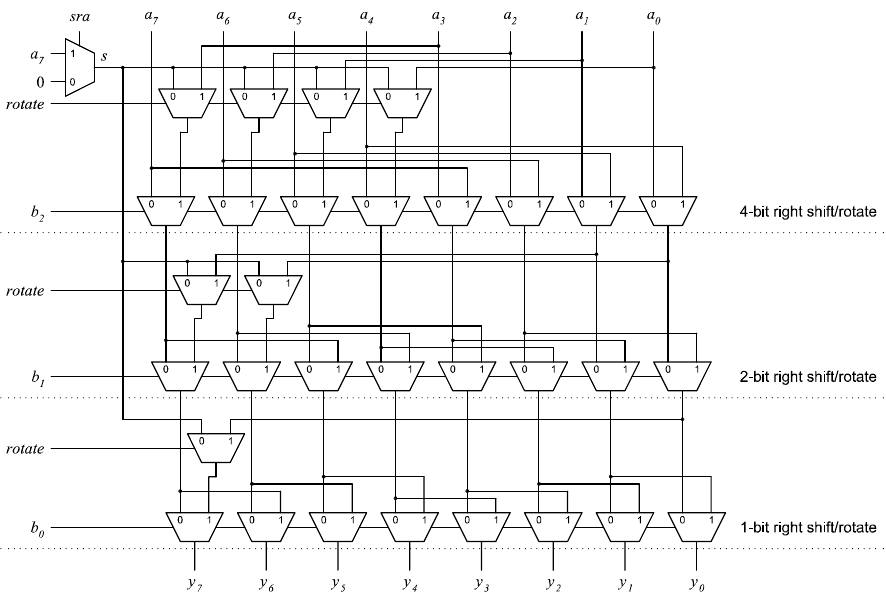
Barrel shift/rotate

---

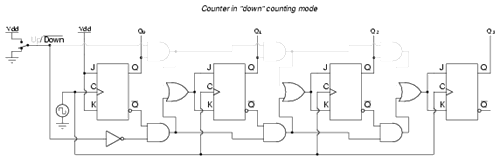
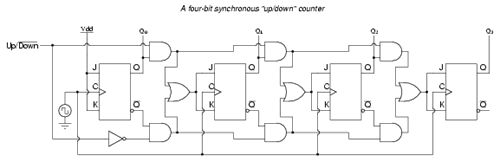
Synchronous up/down counter

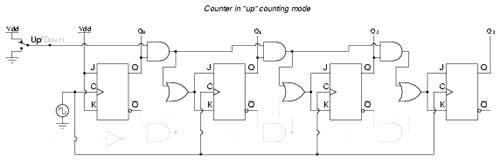
Up counting

Down counting

---