Circular Arc Segmentation

(Based on Approximate Digital Circularity)

Algorithm

Partha Bhowmick and Shyamosree Pal, Fast Circular Arc Segmentation Based on Approximate Circularity and Cuboid Graph, Journal of Mathematical Imaging and Vision (Springer), Vol. 49(1), pp. 98-122, 2014.

The Idea

Based on approximate circularity, cuboid graph in the 3D parameter space, and delimited cliques in the cuboid graph forming larger arcs. As circular arcs present in real-world images often deviate from the ideal conditions of digital circularity, we have loosened their parameter range by an adaptive tolerance. Approximate circularity is thus realized by modifying certain number-theoretic properties of digital circularity. Owing to integer computation and judiciousness of delimited cliques, the algorithm runs very fast even for very large images.

Why Approximate Circularity

The following example shows why approximate circularity is required to allow slight deviation of run lengths.
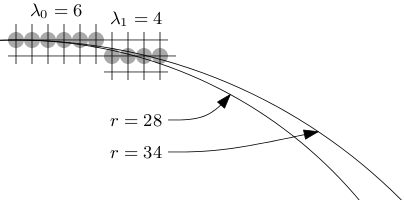
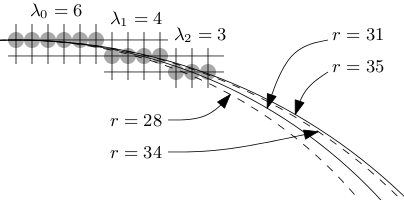
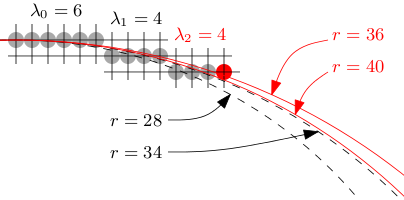
For λ0 = 6 and λ1 = 4, we have Λ1 = 6 + 4 = 10, and so the radius interval [r, r] becomes [28, 34]. If the next run has λ2 = 3, then Λ2 = Λ1 + λ2 = 13, and so the new radius interval becomes [s, s] = [31, 35] whose intersection with the previous interval is [28, 34]∩[31, 35] = [31, 34] (nonempty). However, if λ2 = 4, then [s, s] = [36, 40], which has an empty intersection with [r, r], implying that the sequence 6, 4, 4 is not (exactly) "digitally circular". 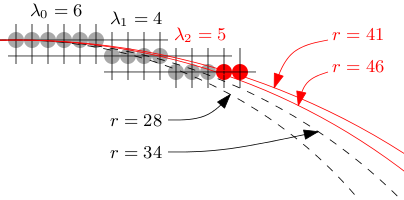If λ2 = 5, then [s, s] = [41, 46], and its intersection with [r, r] is not only empty, but also moves further off.

Algorithms





Demonstration of FINDDELIMITEDCLIQUES on the Cuboid Graph


(a) Unprocessed vertices are shown in bright yellow and unexplored edges in light gray. (b) The vertex initiating a 4-clique is shown in red, its adjacent vertices in bright yellow with the corresponding edges in black, and all other vertices and edges shown dimmed. (c, d) Recursive development with the vertices initiating the non-maximal and smaller cliques shown in red when the recursion progresses, and shown in blue while coming out of the recursion. The blue vertices are actually added to K and deleted from U in Steps 6 and 7 of FindDisjoint-k-Cliques. (e) The 4-clique. (f) Initiating step to find a 3-clique. (g) Recursive development to obtain the 3-clique (green vertices) and the residual 1-clique (red vertex).


Step-by-step Results

Click on the image to see in full scale.


Input image.

Extremum runs (red) with the effective midpoints marked in black on the thinned image.

Arcs detected in different octants (odd-numbered octants shown in red and even-numbered octants in blue).


Arcs after pairing by extremum runs. Types T and B are shown in red, and L and R in blue.

Final output by our algorithm. 4-cliques are shown in blue, 3- or 2-cliques in green, and 1-cliques in red. Points in light gray are reported as not lying on any circular arc.

More Results
A pdf with results on industrial images.
Average CPU time to process an image of size 1000×1000 after binarization is less than 0.5 second.