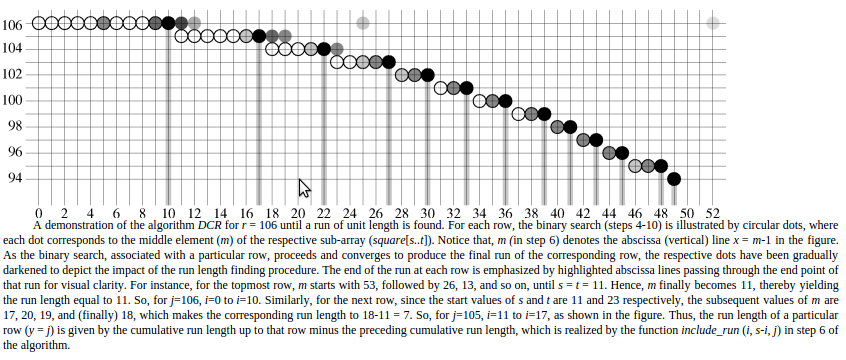
DCS
 Digital circles, abiding with their weird and challenging nature in the discrete domain, have drawn immense research interest since the early adoption of the scan-conversion technique for their efficient approximation from the continuous domain to the digital domain. Subsequent improvements of these algorithms meant for generation of circular arcs were achieved by different researchers in the later periods. Further, apart from the circle-generation algorithms, since the properties, parameterization, characterization, and recognition of digital circles and circular arcs shape up a very engrossing area of research, several other interesting works on digital circles and related problems have also appeared from time to time.
However, the essence of all these algorithms is that, although a circle drawing algorithm primarily originates from the naive concept of intelligent digital applications of first-order and second-order derivatives (differences) as in Bresenham's, a digital circle is endowed with some other interesting properties contributed by the classical theories in the discrete domain. It has been gradually made apparent from these works that digital circles, similar to digital straight lines, possess some striking characteristics, which, if interpreted rightly and exploited properly, may produce interesting results and scope for subsequent potential applications in the discrete domain.
Our number-theoretic interpretation reveals the relation between perfect squares (square numbers) in discrete (integer) intervals and few interesting and useful properties of a digital circle. Based on these number-theoretic properties, the problem of constructing a digital circle or a circular arc maps to the new domain of number theory. However, the construction of a digital circle using these properties should not be looked upon as a competition with Bresenham's algorithm or any other similar algorithm; rather, these number-theoretic properties enrich the understanding of digital circles from a perspective that is different from the customary aspects of digital calculus. We have also shown how these intervals can be obtained for the given radius of a circle, and what effects these intervals have on the construction of a digital circle.
Digital circles, abiding with their weird and challenging nature in the discrete domain, have drawn immense research interest since the early adoption of the scan-conversion technique for their efficient approximation from the continuous domain to the digital domain. Subsequent improvements of these algorithms meant for generation of circular arcs were achieved by different researchers in the later periods. Further, apart from the circle-generation algorithms, since the properties, parameterization, characterization, and recognition of digital circles and circular arcs shape up a very engrossing area of research, several other interesting works on digital circles and related problems have also appeared from time to time.
However, the essence of all these algorithms is that, although a circle drawing algorithm primarily originates from the naive concept of intelligent digital applications of first-order and second-order derivatives (differences) as in Bresenham's, a digital circle is endowed with some other interesting properties contributed by the classical theories in the discrete domain. It has been gradually made apparent from these works that digital circles, similar to digital straight lines, possess some striking characteristics, which, if interpreted rightly and exploited properly, may produce interesting results and scope for subsequent potential applications in the discrete domain.
Our number-theoretic interpretation reveals the relation between perfect squares (square numbers) in discrete (integer) intervals and few interesting and useful properties of a digital circle. Based on these number-theoretic properties, the problem of constructing a digital circle or a circular arc maps to the new domain of number theory. However, the construction of a digital circle using these properties should not be looked upon as a competition with Bresenham's algorithm or any other similar algorithm; rather, these number-theoretic properties enrich the understanding of digital circles from a perspective that is different from the customary aspects of digital calculus. We have also shown how these intervals can be obtained for the given radius of a circle, and what effects these intervals have on the construction of a digital circle.
Source : http://cse.iitkgp.ac.in/~pb/research-pbhowmick.html


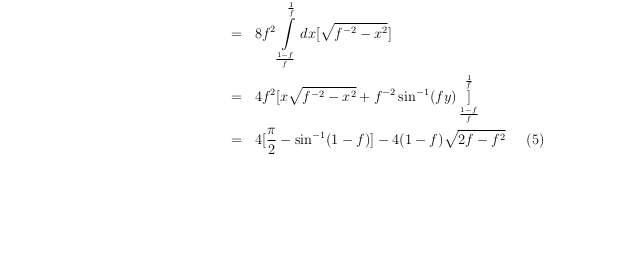
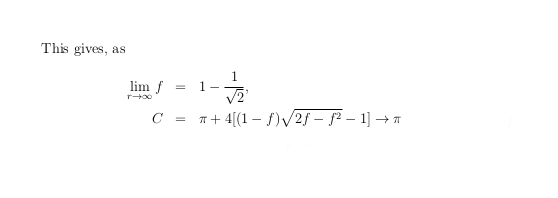
 Digital circles, abiding with their weird and challenging nature in the discrete domain, have drawn immense research interest since the early adoption of the scan-conversion technique for their efficient approximation from the continuous domain to the digital domain. Subsequent improvements of these algorithms meant for generation of circular arcs were achieved by different researchers in the later periods. Further, apart from the circle-generation algorithms, since the properties, parameterization, characterization, and recognition of digital circles and circular arcs shape up a very engrossing area of research, several other interesting works on digital circles and related problems have also appeared from time to time.
However, the essence of all these algorithms is that, although a circle drawing algorithm primarily originates from the naive concept of intelligent digital applications of first-order and second-order derivatives (differences) as in Bresenham's, a digital circle is endowed with some other interesting properties contributed by the classical theories in the discrete domain. It has been gradually made apparent from these works that digital circles, similar to digital straight lines, possess some striking characteristics, which, if interpreted rightly and exploited properly, may produce interesting results and scope for subsequent potential applications in the discrete domain.
Our number-theoretic interpretation reveals the relation between perfect squares (square numbers) in discrete (integer) intervals and few interesting and useful properties of a digital circle. Based on these number-theoretic properties, the problem of constructing a digital circle or a circular arc maps to the new domain of number theory. However, the construction of a digital circle using these properties should not be looked upon as a competition with Bresenham's algorithm or any other similar algorithm; rather, these number-theoretic properties enrich the understanding of digital circles from a perspective that is different from the customary aspects of digital calculus. We have also shown how these intervals can be obtained for the given radius of a circle, and what effects these intervals have on the construction of a digital circle.
Digital circles, abiding with their weird and challenging nature in the discrete domain, have drawn immense research interest since the early adoption of the scan-conversion technique for their efficient approximation from the continuous domain to the digital domain. Subsequent improvements of these algorithms meant for generation of circular arcs were achieved by different researchers in the later periods. Further, apart from the circle-generation algorithms, since the properties, parameterization, characterization, and recognition of digital circles and circular arcs shape up a very engrossing area of research, several other interesting works on digital circles and related problems have also appeared from time to time.
However, the essence of all these algorithms is that, although a circle drawing algorithm primarily originates from the naive concept of intelligent digital applications of first-order and second-order derivatives (differences) as in Bresenham's, a digital circle is endowed with some other interesting properties contributed by the classical theories in the discrete domain. It has been gradually made apparent from these works that digital circles, similar to digital straight lines, possess some striking characteristics, which, if interpreted rightly and exploited properly, may produce interesting results and scope for subsequent potential applications in the discrete domain.
Our number-theoretic interpretation reveals the relation between perfect squares (square numbers) in discrete (integer) intervals and few interesting and useful properties of a digital circle. Based on these number-theoretic properties, the problem of constructing a digital circle or a circular arc maps to the new domain of number theory. However, the construction of a digital circle using these properties should not be looked upon as a competition with Bresenham's algorithm or any other similar algorithm; rather, these number-theoretic properties enrich the understanding of digital circles from a perspective that is different from the customary aspects of digital calculus. We have also shown how these intervals can be obtained for the given radius of a circle, and what effects these intervals have on the construction of a digital circle.
