Performance analysis of programs
There may exist many algorithms to solve a given problem. Moreover, the same algorithm may be implemented in a variety of ways. It is now time to analyze the relative merits and demerits of different algorithms and of different implementations. We are shortly going to introduce a set of theoretical tools that make this analysis methodical. In order to solve a problem, it is not sufficient to design an algorithm and provide a correct (bug-free) implementation of the algorithm. One should also understand how good his/her program is. Here "goodness" is measured by relative performance of a program compared to other algorithms and implementations. This is where the true "computer science" starts. Being able to program does not qualify one to be a computer scientist or engineer. A good programmer is definitely a need for every modern society and it requires time and patience to master the art of good programming. Computer science goes beyond that by providing formal treatment of programs and algorithms. Consider that an airplane pilot is not required to know any aerospace engineering and an aerospace engineer need not know how to run an airplane. We need both pilots and aerospace engineers for our society.
In short, when you write (and perhaps sell) your programs or when you buy others' programs, you should exercise your ability to compare the apparent goodness of available programs. The task is not always easy. Here are some guidelines for you.
Resource usage of a program
You may feel tempted to treat a small and compact program as good. That is usually not a criterion for goodness. Most users execute precompiled binaries. It does not matter how the source code looked like. What is more important is how efficiently a program solves a problem. Efficiency, in turn, is measured by the resource usage of a program (or algorithm). The two most important general resources are:
- Running time
- Space requirement
Here running time refers to the amount of time taken by a program for a given input. The time is expected to vary according to what input the program processes. For example, a program that does matrix multiplication should take more running time for bigger matrices. It is, therefore, customary to view the running time as a function of the input. In order to simplify matters, we assume that the size of the input is the most important thing (instead of the actual input). For instance, a standard matrix multiplication routine performs a number of operations (additions and multiplications of elements) that is dependent only on the dimensions of the input matrices and not on the actual elements of the matrices.
A standard practice is to measure the size of the input by the number of bits needed to represent the input. However, this simple convention is sometimes violated. For example, when an array of integers need be sorted, it is customary to take the size of the array (number of integers in the array) as the input size. Under the assumption that each integer is represented by a word of a fixed size (e.g. 32 bits), the bit-size of the input is actually a constant multiple of the array size, and so this new definition of input size is not much of a deviation from the standard convention. (We will soon see that constant multipliers are neglected in the theory.) However, when the integers to be sorted may be arbitrarily large (multiple precision integers), this naive negligence of the sizes of the operands is certainly not a good idea. One should in this case consider the actual sizes (in bits or words) of each individual element of the array.
Poorer measures of input size are also sometimes adopted. An nxn matrix contains n2 elements and even if each element is of fixed size (like int or float), one requires a number of bits proportional to n2 for the complete specification of the matrix. However, when we plan to multiply two nxn matrices or invert an nxn matrix, it is seemigly more human to treat n (instead of n2) as the input size parameter. In other words, the running time is expressed as a function of n and not as a function of the technically correct input size n2 (though they essentially imply the same thing).
Space (memory) requirement of a program is the second important criterion for measuring the performance of a program. Obviously, a program requires space to store (and subsequently process) the input. What matters is the additional amount of memory (static and dynamic) used by the program. This extra storage is again expressed as a function of the input size.
It is often advisable to reduce the space requirement of a program. Earlier, semiconductor memory happenned to be a costly resource and so programs requiring smaller amount of extra memory are prefered to programs having larger space requirements. Nowadays, the price of semiconductor memory has gone down quite dramatically. Still, a machine comes with only a finite amount of memory. This means that a program having smaller space requirement can handle bigger inputs given any limited amount of memory. The essential argument in favor of reducing the space requirement of a program continues to make sense today and will do so in any foreseeable future.
Some other measures of performance of a program may be conceived of, like ease of use (the user interface), features, security, etc. These requirements are usually application-specific. We will not study them in a general forum like this chapter.
Palatable and logical as it sounds, it is difficult to express the running time and space usage of a program as functions of the input size. The biggest difficulty is to choose a unit of time (or space). Since machines vary widely in speed and memory management issues, the same program running on one machine may have markedly different performance figures on another machine. A supercomputer is expected to multiply two given matrices much faster than a PC. There is no standard machine for calibrating the relative performances of different programs. Comparison results on a particular machine need not tally with the results on a different machine. Since different machines have different CPU and memory organizations and support widely varying instruction sets, results from one machine cannot, in general, be used to predict program behaviors on another machine. That's a serious limitation of machine-dependent performance figures.
There is a hell lot of other factors that lead to variations in the running time (and space usage) of a program, even when the program runs on the same machine. These variations are caused by off-line factors (like the compiler used to compile the program), and also by many run-time factors (like the current load of the CPU, the current memory usage, availability of cache memory and swap memory).
To sum up, neither seconds (or its fractions like microseconds) nor machine cycles turn out to be a faithful measure of the running time of a program. Similarly, memory usage cannot be straightaway measured in bits or words. We must invent some kind of abstractions. The idea is to get rid of the dependence on the run-time environment (including hardware). A second benefit is that we don't have to bother about specific implementations. An argument in the algorithmic level would help us solve our problem of performance measurement.
The abstraction is based on the measurement of time by numbers. Such a number signifies the count of basic operations performed by the program (or algorithm). A definition of what is basic will lead to controversies. In order to avoid that, we will adopt our own conventions. An arithmetic operation (addition, subtraction, multiplication, division, comparison, etc. of integers or floating point numbers) will be treated as a basic operation. So will be a logical and a bitwise operation (AND, OR, shift etc.). We will count (in terms of the input size) how many such basic operations are performed by the program. That number will signify the abstract running time of the program. Usually, the actual running times of different programs are closely proportional to these counts. The constant of proportionality depends on the factors mentioned above and vary from machine to machine (and perhaps from time to time on the same machine). We will simply ignore these constants. This practice will bring under the same umbrella two programs doing n2 and 300n2 basic operations respectively for solving the same problem. Turning blind to constants of proportionality is not always a healthy issue. Nonetheless, the solace is that these abstract measures have stood the taste of time in numerous theoretical and practical situations.
The space requirement of a program can be quantified along similar lines, namely, by the number of basic units (integers or floating-point numbers or characters) used by a program. Again we ignore proportionality constants and do not talk about the requirement of memory in terms of bits.
We will call the above abstract running time and space usage of a program to be its time complexity and space complexity respectively. In the rest of this chapter, we will concentrate mostly on time complexity.
The order notation
The order notation captures the idea of time and space complexities in precise mathematical terms. Let us start with the following important definition:
Let f and g be two positive real-valued functions on the set N of natural numbers. We call g(n) to be of the order of f(n) if there exist a positive real constant c and a natural number n0 such that g(n) <= cf(n) for all n >= n0. In this case we write g(n) = O(f(n)) and also say that g(n) is big-Oh of f(n). |
The following figure illustrates the big-Oh notation. In this example, we take c=2.
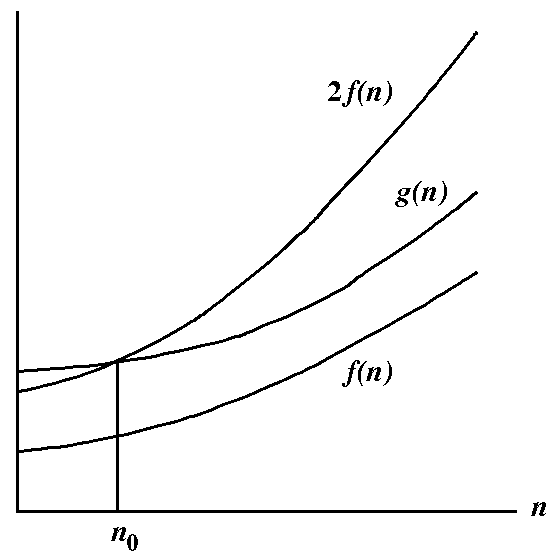
Figure: Explaining the big-Oh notation
Examples
- Take f(n) = n and g(n) = 2n + 3. For n >= 3 we have 2n + 3 <= 3n. Thus taking the constants c = 3 and n0 = 3 shows that 2n + 3 = O(n). Conversely, for any n >= 1 we have n <= 2n + 3, i.e., n = O(2n + 3) too.
- Since 100n <= n2 for all n >= 100, we have 100n = O(n2). Now I will show that n2 is not of the order of 100n. Assume otherwise, i.e., n2 = O(100n), i.e., there exist constants c and n0 such that n2 <= 100cn for all n >= n0. This implies that n <= 100c for all n >= n0. This is clearly absurd, since c is a finite positive real number.
- The last two examples can be easily generalized. Let f(n)
be a polynomial in n of degree d. It can be easily shown
that f(n) = O(nd). In other words, the highest degree
term in a polynomial determines its order. That is intuitively clear,
since as n becomes sufficiently large, the largest degree
term dominates over other terms.
Now let g(n) be another polynomial in n of degree e. Assume that d <= e. Then it can be shown that f(n) = O(g(n)). If d = e, then g(n) = O(f(n)) too. However, if d < e, then g(n) is not O(f(n)).
Any function that is O(nd) for some positive integral constant d is said to be of polynomial order. A function which is O(n) is said to be of linear order. We can analogously define functions of quadratic order (O(n2) functions), cubic order (O(n3) functions), and so on.
- A distinguished case of polynomial order O(nd) corresponds to the value d = 0. A function f(n) of this order is an O(1) function. For all sufficiently big n, f(n) is by definition bounded from above by a constant value and so is said to have constant order.
- I will now show n = O(2n). We prove by induction
on n that n <= 2n for all n >= 1.
This is certainly true for n = 1. So assume that n >= 2 and
that n - 1 <= 2n-1. We also have 1 <= 2n-1.
Adding the two inequalities gives n <= 2n.
The converse of the last order relation is not true, i.e., 2n is not of the order of n. We prove this by contradiction. Assume that 2n = O(n), i.e., 2n <= cn for all n >= n0. Simple calculus shows that the function 2x / x on a real variable x tends to infinity as x tends to infinity. In particular, c cannot be a bounded constant in this case.
A function which is O(an) for some real constant a > 1 is said to be of exponential order. It can be shown that for any a > 1 and d >= 1 we have nd = O(an), but an is not of the order of nd. In other words, any polynomial function grows more slowly than a (truly) exponential function.
- A similar comparison holds between logarithmic and polynomial functions. For any positive integers d and e, the function (log n)d is O(ne), but ne is not O((log n)d). Functions of polynomial, exponential and logarithmic orders are most widely used for analyzing algorithms.
We now explain how the order notation is employed to characterize the time and space complexities of a program. We count the number of basic operations performed by an algorithm and express that count as having the order of a simple function. For example, if an algorithm performs 2n2 - 3n + 1 operations on an input of size n, we say that the algorithm runs in O(n2) time, i.e., in quadratic time, or that it is a quadratic time algorithm. Any algorithm that runs in polynomial time is said to be a polynomial-time algorithm. An algorithm that does not run in polynomial time, but in exponential time, is called an exponential-time algorithm. An exponential function (like 2n) grows so rapidly (compared to polynomial functions) with the input n that exponential-time algorithms are usually much slower compared to polynomial-time algorithms, even when the input is not too big. By an efficient solution of a problem, one typically means devising an algorithm for that problem, that runs in some polynomial time O(nd) with d as small as possible.
Examples
We now analyze the complexities of some popular algorithms discussed earlier in the notes.
- Computation of factorials
In this case we express the running-time as a function of the integer n whose factorial is to be computed. Let us first look at the following iterative algorithm:
int factorialIter ( int n ) { int prod, i; if (n <= 1) return 1; prod = 1; for (i=2; i<=n; ++i) prod *= i; return prod; }The function first compares n with 1. If n is indeed less than or equal to 1, the constant value 1 is returned. Thus for n = 0,1 the algorithm does only one basic operation (comparison). Here we neglect the cost of returning a value. If n > 2, then prod is first initialized to 1. Then the loop starts. The loop contains an initialization of i, exactly n-1 increments of i and exactly n comparisons of i with n. Inside the function body the variable prod is multiplied by i. The loop is executed n-1 times. This accounts for a total of n-1 multiplications. Thus the total number of basic operations done by this iterative function is
1 + 1 + 1 + (n-1) + n + (n-1) = 3n + 1.
Since 3n + 1 is O(n), it follows that the above algorithm runs in linear time.
Next consider the following recursive function for computing factorials:
int factorialRec ( int n ) { if (n <= 1) return 1; return n * factorialRec(n-1); }Let T(n) denote the running time of this recursive algorithm for the input n. If n = 0,1, then T(n) = 1, since computation in these cases involves only a single comparison. If n >= 2, then in addition to this comparison, factorialRec is called on input n-1 and then the return value is multiplied by n. To sum up, we have:
T(0) = 1, T(1) = 1, T(n) = 1 + T(n-1) + 1 = T(n-1) + 2 for n >= 2.
This is not a closed-form expression for T(n). A formula for T(n) can be derived by repeatedly using the last relation until the argument becomes too small (0 or 1) so that the constant value 1 can be substitued for it.
T(n) = T(n-1) + 2 = (T(n-2) + 2) + 2 = T(n-2) + 4 = T(n-3) + 6 ... = T(1) + 2(n-1) = 1 + 2(n-1) = 2n - 1.Therefore,T(0) = 1, T(n) = 2n - 1 for n >= 1.
It follows that the recursive function also runs in linear time. Note that both the iterative and recursive versions run in O(n) time. But the actual running times are respectively 3n + 1 and 2n - 1. It may appear to the reader that the recursive function is faster (since 2 is smaller than 3). But in the analysis, we have neglected the cost of function calls and returns. The iterative version makes no recursive calls, whereas the recursive version makes n-1 recursive calls. It depends on the compiler and the run-time system whether n-1 recursive calls is slower or faster than the overhead associated with the loop in the iterative version. Still, we should feel happy to end the story by rephrasing the fact that both the two versions are equally efficient -- as efficient as an O(n) function.
- Computation of Fibonacci numbers
With Fibonacci numbers, the iterative and recursive versions exhibit marked difference in running times. We start with the iterative version.
int fibIter ( int n ) { int i, p1, p2, F; if (n <= 1) return n; i = 1; F = 1; p1 = 0; while (i < n) { ++i; p2 = p1; p1 = F; F = p1 + p2; } return F; }The function initially makes a comparison and if n = 0,1 the value n is returned. For n >= 2, it proceeds further down. First, three variables (i,F,p1) are initialized. The subsequent while loop is executed exactly n-1 times. The body of the loop involves four basic operations (one increment, two copies and one addition). Moreover, the loop continuation condition is checked n times. So the number of basic operations performed by this iterative algorithm is
1 + 3 + 4(n-1) + n = 5n.
In particular, fibIter runs in linear time.
Let us now investigate the recursive version:
int fibRec ( int n ) { if (n <= 1) return n; return fibRec(n-1) + fibRec(n-2); }Let T(n) denote the running time of this recursive function on input n. Simple investigation of the function shows that:
T(0) = 1, T(1) = 1, T(n) = T(n-1) + T(n-2) + 2 for n >= 2.
Now it is somewhat complicated to find a closed-form formula for T(n). We instead give an upper bound and a lower bound on T(n). To that effect let us first introduce a new function S(n) as:
S(n) = T(n) + 2 for all n.
We then have:
S(0) = 3, S(1) = 3, S(n) = S(n-1) + S(n-2) for n >= 2.
Denote by F(n) the n-th Fibonacci number and use induction on n. S(0) <= F(4) and S(1) <= F(5). Moreover, S(n) = S(n-1) + S(n-2) <= F(n+3) + F(n+2) = F(n+4). A lower bound on S(n) can be derived by induction on n as: S(0) >= F(3) and S(1) >= F(4). Moreover, S(n) = S(n-1) + S(n-2) >= F(n+2) + F(n+1) = F(n+3). It follows that:
F(n+3) - 2 <= T(n) <= F(n+4) - 2 for all n >= 0.
The next question is to find a closed form formula for the Fibonacci numbers. We will not do it here, but present the well-known result:
F(n) = [1/sqrt(5)][((1+sqrt(5))/2)n - ((1-sqrt(5))/2)n].
The number r = (1+sqrt(5))/2 = 1.61803... is called the golden ratio. Also (1-sqrt(5))/2 = -0.61803... is the negative of the reciprocal of the golden ratio and has absolute value less than 1. The powers [(1-sqrt(5))/2]n become very small for large values of n and so
F(n) is approximately equal to [1/sqrt(5)]rn.
For all sufficiently large n, we then have
[1/sqrt(5)]rn+3 - 2 <= T(n) <= [1/sqrt(5)]rn+4 - 2
The first inequality shows that T(n) cannot have polynomial order, whereas the second inequality shows that T(n) is of exponential order.
To sum up, recursion helped us convert a polynomial-time (in fact, linear) algorithm to a truly exponential algorithm. This teaches you two lessons. First, use recursion judiciously. Second, different algorithms (or implementations) for the same problem may have widely different complexities. Performance analysis of programs is really important then!
- Linear search
We are given an array A of n integers and another integer x. The task is to locate the existence of x in A. Here n is taken to be the input size. We assume that A is not sorted, i.e., we will do linear search in the array. Here is the code:
int linSearch ( int A[] , int n , int x ) { int i; for (i=0; i<n; ++i) if (A[i] == x) return 1; return 0; }The time complexity of the above function depends on whether x is present in A and if so at which location. Clearly, the worst case (longest running time) occurs when x is not present in the array and the last statement (return 0;) is executed. In this case the loop requires one initialization of i, n increments of i and n+1 comparisons of i with n. Inside the loop body there is a single comparison which fails in all of the n iterations of the loop in the worst-case scenario. Thus the total time needed by this function is:
1 + n + (n+1) + n = 3n + 2.
This is O(n), i.e., the linear search is a linear time algorithm.
- Binary search
In order to curtail the running time of linear search, one uses the binary search algorithm. This requires the array A to be sorted a priori. We do not compute the running time for sorting now, but look at the running time of binary search in a sorted array.
int binSearch ( int A[] , int n , int x ) { int L, R, M; L = 0; R = n-1; while (L < R) { M = (L + R) / 2; if (x > A[M]) L = M+1; else R = M; } return (A[L] == x); }For simplicity assume that the array size n is a power of 2, i.e., n = 2k for some integer k >= 0. Initially, the boundaries L and R are adjusted to the leftmost and rightmost indices of the entire array. After each iteration of the while loop the central index M of the current search window is computed. Depending on the result of comparison of x with A[M], the boundaries (L,R) is changed either to (L,M) or to (M+1,R). In either case, the size of the search window (i.e., the subarray delimited by L and R) is reduced to half. Thus after k iterations of the while loop the search window reduces to a subarray of size 1, and L and R become equal. After the loop terminates, a comparison is made between x and an array element. So the number of basic operations done by this algorithm equals:
2 + (k+1) + k x (2 + 1 + 1) + 1 (Init) (Loop condn) (No of iter) (ops in loop body) (last comparison) = 5k + 4.But k = log2n, so the running time of binary search is O(log n), i.e., logarithmic. This is far better than the linear running time of the linear search algorithm.
- Bubble sort
It is interesting to look at the running times of different sorting algorithms. Let us start with a non-recursive sorting algorithm. Here is the code that bubble sorts an array of size n.
void bubbleSort ( int A[] , int n ) { for (i=n-2; i>=0; --i) { for (j=0; j<=i; ++j) { if (A[j] > A[j+1]) { t = A[j]; A[j] = A[j+1]; A[j+1] = t; } } } }This is an example of a nested for loop. The outer loop runs over i for the values n-2,n-3,...,0 and for a value of i the inner loop is executed i+1 times. This means that the inner loop is executed a total number of
(n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2
times. Each iteration of the inner loop involves a comparison and conditionally a set of three assignment operations. Thus the inner loop performs at most
4 x n(n-1)/2 = 2n(n-1)
basic operations. This quantity is O(n2). We should also add the costs associated with the maintenance of the loops. The outer loop requires O(n) time, whereas for each i the inner loop requires O(i) time. The n-1 iterations of the outer loop then leads to a total of O((n-1) + (n-2) + ... + 1), i.e., O(n2), basic operations for maintaining all of the inner loops. To sum up, we conclude that the bubble sort algorithm runs in O(n2) time.
- Matrix multiplication
Here is the straightforward code for multiplying two n x n matrices. We take n as the input size parameter.
/* Multiply two n x n matrices A and B and store the product in C */ void matMul ( int C[SIZE][SIZE] , int A[SIZE][SIZE] , int B[SIZE][SIZE] , int n ) { int i, j, k; for (i=0; i<n; ++i) { for (j=0; j<n; ++j) { C[i][j] = 0; for (k=0; k<n; ++k) C[i][j] += A[i][k] * B[k][j]; } } }This is another example of nested loops with an additional level of nesting (compared to bubble sort). The outermost and the intermediate loops run independently over the values of i and j in the range 0,1,...,n-1. For each of these n2 possible values of i,j, the element C[i][j] is first initialized and then the innermost loop on k is executed exactly n times. Each iteration in the innermost loop involves one multiplication and one addition. Therefore, for each i,j the innermost loop takes O(n) running time. This is also the cost associated with maintaining the loop on k. Thus each execution of the body of the intermediate loop takes a total of O(n) time and this body is executed n2 times leading to a total running time of O(n3). It is easy to argue that the cost for maintaining the loop on i is O(n) and that for maintaining all of the n executions of the intermediate loop is O(n2).
So two n x n matrices can be multiplied in O(n3) time. Can we make any better than that? The answer is: yes. There are algorithms that multiply two n x n matrices in time O(nw) time, where w < 3. One example is Straßen's algorithm that takes time O(nlog2(7)), i.e., O(n2.807...). The best known matrix multiplication algorithm is due to Coppersmith and Winograd. Their algorithm has a running time of O(n2.376). It is clear that for setting the value of all C[i][j]'s one must perform at least n2 basic operations. It is still an open question whether O(n2) running time suffices for matrix multiplication.
- Stack ADT operations
Look at the two implementations of the stack ADT detailed earlier. It is easy to argue that each function (except print) performs only a constant number of operations irrespective of the current size of the stack and so has a running time of O(1). This is the reason why we planned to write seperate routines for the stack and queue ADTs instead of using the routines for the ordered list ADT. Insertion or deletion in the ordered list ADT may require O(n) time, where n is the current size of the list.
- Partitioning in quick sort
This example illustrates the space complexity of a program (or function). We concentrate only on the partitioning stage of the quick sort algorithm. The following function takes the first element of the array as the pivot and returns the last index of the smaller half of the array. The pivot is stored at this index.
int partition1 ( int A[] , int n ) { int *L, *R, lIdx, rIdx, i, pivot; L = (int *)malloc((n-1) * sizeof(int)); R = (int *)malloc((n-1) * sizeof(int)); pivot = A[0]; lIdx = rIdx = 0; for (i=1; i<n; ++i) { if (A[i] <= pivot) L[lIdx++] = A[i]; else R[rIdx++] = A[i]; } for (i=0; i<lIdx; ++i) A[i] = L[i]; A[lIdx] = pivot; for (i=0; i<rIdx; ++i) A[lIdx + 1 + i] = R[i]; free(L); free(R); return lIdx; }Here we collect elements of A[] smaller than or equal to the pivot in the array L and those that are larger than the pivot in the array R. We allocate memory for these additional arrays. Since the sizes of L and R are not known a priori, we have to prepare for the maximum possible size (n-1) for both. In addition, we use a constant number (six) of variables. The total additional space requirement for this function is therefore
2(n-1) + 6 = 2n + 4,
which is O(n).
Let us plan to reduce this space requirement. A possible first approach is to store L and R in a single array LR of size n-1. Though each of L and R may be individually as big as having a size of n-1, the total size of these two arrays must be n-1. We store elements of L from the beginning and those of R from the end of LR. The following code snippet incorporates this strategy:
int partition2 ( int A[] , int n ) { int *LR, lIdx, rIdx, i, pivot; LR = (int *)malloc((n-1) * sizeof(int)); pivot = A[0]; lIdx = 0; rIdx = n-1; for (i=1; i<n; ++i) { if (A[i] <= pivot) LR[lIdx++] = A[i]; else LR[rIdx--] = A[i]; } for (i=0; i<lIdx; ++i) A[i] = LR[i]; A[lIdx] = pivot; for (i=rIdx+1; i<n; ++i) A[i] = LR[i]; free(LR); return lIdx; }The total amount of extra memory used by this function is
(n-1) + 5 = n + 4,
which, though about half of the space requirement for partition1, is still O(n).
We want to reduce the space complexity further. Using one or more additional arrays will always incur O(n) space overhead. So we would avoid using any such extra array, but partition A in A itself. This is called in-place partitioning. The function partition3 below implements in-place partitioning. It works as follows. It maintains the loop invariant that at all time the array A is maintained as a concatenation LUR of three regions. The leftmost region L contains elements smaller than or equal the pivot. The rightmost region R contains elements bigger than the pivot. The intermediate region U consists of yet unprocessed elements. Initially, U is the entire array A (or A without the first element which is taken to be the pivot), and finally U should be empty. The region U is delimited by two indices lIdx and rIdx indicating respectively the first and last indices of U. During each iteration, the element at lIdx is compared with the pivot, and depending on the comparison result this element is made part of L or R.
int partition3 ( int A[] , int n ) { int lIdx, rIdx, pivot, t; pivot = A[0]; lIdx = 1; rIdx = n-1; while (lIdx <= rIdx) { if (A[lIdx] <= pivot) { /* The region L grows */ ++lIdx; } else { /* Exchange A[lIdx] with the element at the U-R boundary. */ t = A[lIdx]; A[lIdx] = A[rIdx]; A[rIdx] = t; /* The region R grows */ --rIdx; } } /* Place the pivot A[0] in the correct place by exchanging it with the last element of L */ A[0] = A[rIdx]; A[rIdx] = pivot; return rIdx; }The function partition3 uses only four extra variables and so its space complexity is O(1). That is a solid improvement over the earlier versions.
It is easy to check that the time complexity of each of these three partition routines is O(n).
Worst-case versus average complexity
Our basic aim is to provide complexity figures (perhaps in the O notation) in terms of the input size, and not as a function of any particular input. So far we have counted the maximum possible number of basic operations that need be executed by a program or function. As an example, consider the linear search algorithm. If the element x happens to be the first element in the array, the function linSearch returns after performing only few operations. The farther x can be located down the array, the bigger is the number of operations. Maximum possible effort is required, when x is not at all present in the array. We argued that this maximum value is O(n). We call this the worst-case complexity of linear search.
There are situations where the worst-case complexity is not a good picture of the practical situation. On an average, a program may perform much better than what it does in the worst case. Average complexity refers to the complexity (time or space) of a program (or function) that pertains to a random input. It turns out that average complexities for some programs are markedly better than their worst-case complexities. There are even examples where the worst-case complexity is exponential, whereas the average complexity is a (low-degree) polynomial. Such an algorithm may take a huge amount of time in certain esoteric situations, but for most inputs we expect the program to terminate soon.
We provide a concrete example now: the quick sort algorithm. By partition we mean a partition function for an array of n integers with respect to the first element of the array as the pivot. One may use any one of the three implementations discussed above.
void quickSort ( int A[] , int n )
{
int i;
if (n <= 1) return;
i = partition(A,n); /* Partition with respect to A[0] */
quickSort(A,i); /* Recursively sort the left half excluding the pivot */
quickSort(&A[i+1],n-i-1); /* Recursively sort the right half */
}
Let T(n) denote the running time of quickSort for an array of n integers. The running time of the partition function is O(n). It then follows that:
T(n) <= T(i) + T(n-i-1) + cn + d
for some constants c and d and for some i depending on the input array A. The presence of i on the right side makes the analysis of the running time somewhat difficult. We cannot treat i as a constant for all recursive invocations. Still, some general assumptions lead to easily derivable closed-form formulas for T(n).
An algorithm like quick sort (or merge sort) is called a divide-and-conquer algorithm. The idea is to break the input into two or more parts, recursively solve the problem on each part and subsequently combine the solutions for the different parts. For the quick sort algorithm the first step (breaking the array into two subarrays) is the partition problem, whereas the combining stage after the return of the recursive calls involves doing nothing. For the merge sort, on the other hand, breaking the array is trivial -- just break it in two nearly equal halves. Combining the solutions involves the non-trivial merging process.
It follows intuitively that the smaller the size of each subproblem is, the easier it is to solve each subproblem. For any superlinear function f(n) the sum
f(k) + f(n-k-1) + g(n)
(with g(n) a linear function) is large when the breaking of n into k,n-k-1 is very skew, i.e., when one of the parts is very small and the other nearly equal to n. For example, take f(n) = n2. Consider the function of a real variable x:
y = x2 + (n-x-1)2 + g(n)
Differentiation shows that the minimum value of y is attained at x = n/2 approximately. The value of y increases as we move more and more away from this point in either direction.
So T(n) is maximized when i = 0 or n-1 in all recursive calls, for example, when the input array is already sorted either in the increasing or in the decreasing order. This situation yields the worst-case complexity of quick sort:
T(n) <= T(n-1) + T(0) + cn + d
= T(n-1) + cn + d + 1
<= (T(n-2) + c(n-1) + d + 1) + cn + d + 1
= T(n-2) + c[n + (n-1)] + 2d + 2
<= T(n-3) + c[n + (n-1) + (n-2)] + 3d + 3
<= ...
<= T(0) + c[n + (n-1) + (n-2) + ... + 1] + nd + n
= cn(n-1)/2 + nd + n + 1,
which is O(n2), i.e., the worst-case time complexity of quick sort is quadratic.
But what about its average complexity? Or a better question is how to characterize an average case here. The basic idea of partitioning is to choose a pivot and subsequently break the array in two halves, the lesser mortals stay on one side, the greater mortals on the other. A randomly chosen pivot is expected to be somewhere near the middle of the eventual sorted sequence. If the input array A is assumed to be random, its first element A[0] is expected to be at a random location in the sorted sequence. If we assume that all the possible locations are equally likely, it is easy to check that the expected location of the pivot is near the middle of the sorted sequence. Thus the average case behavior of quick sort corresponds to
i = n-i-1 = n/2 approximately.
We than have:
T(n) <= 2T(n/2) + cn + d.
For simplicity let us assume that n is a power of 2, i.e., n = 2t for some positive integer t. But then
T(n) = T(2t)
<= 2T(2t-1) + c2t + d
<= 2(2T(2t-2) + c2t-1 + d) + c2t + d
= 22T(2t-2) + c(2t+2t) + (2+1)d
<= 23T(2t-3) + c(2t+2t+2t) + (22+2+1)d
<= ...
<= 2tT(20) + ct2t + (2t-1+2t-2+...+2+1)d
= 2t + ct2t + (2t-1)d
= cnlog2n + n(d+1) - d.
The first term in the last expression dominates over the other terms and consequently the average complexity of quick sort is O(nlog n).
Recall that bubble sort has a time complexity of O(n2). The situation does not improve even if we assume an average scenario, since we anyway have to make O(n2) comparisons in the nested loop. Insertion and selection sorts attain the same complexity figure. With quick sort, the worst-case complexity is equally poor. But in practice a random array tends to follow the average behavior more closely than the worst-case behavior. That is reasonable improvement over quadratic time. The quick sort algorithm turns out to be one of the practically fastest general-purpose comparison-based sorting algorithm.
We will soon see that even the worst-case complexity of merge sort is O(nlog n). It is an interesting theoretical result that a comparison-based sorting algorithm cannot run in time faster than O(nlog n). Both quick sort and merge sort achieve this lower bound, the first on an average, the second always. Historically, this realization provided a massive impetus to promote and exploit recursion. Tony Hoare invented quick sort and popularized recursion. We cannot think of a modern compiler without this facility.
Also, do you see the significance of the coinage divide-and-conquer?
We illustrated above that recursion made the poly-time Fibonacci routine exponentially slower. That's the darker side of recursion. Quick sort and merge sort highlight the brighter side. When it is your time to make a decision to accept or avoid recursion, what will you do? Analyze the complexity and then decide.
How to compute the complexity of a program?
The final question is then how to derive the complexity of a program. So far you have seen many examples. But what is a standard procedure for deriving those divine functions next to the big-Oh? Frankly speaking, there is none. (This is similar to the situation that there is no general procedure for integrating a function.) However, some common patterns can be identified and prescription solutions can be made available for those patterns. (For integration too, we have method of substitution, integration by parts, and some such standard rules. They work fine only in presence of definite patterns.) The theory is deep and involved and well beyond the scope of this introductory course. We will again take help of examples to illustrate the salient points.
First consider a non-recursive function. The function is a simple top-to-bottom set of instructions with loops embedded at some places in the sequence. One has to carefully study the behavior of the loops and add up the total overhead associated with each loop. The final complexity of the function is the sum of the complexities of each individual instruction (including loops). The counting process is not always straighforward. There is a deadly branch of mathematics, called combinatorics, that deals with counting principles.
We have already deduced the time complexity of several non-recursive functions. Let us now focus our attention to recursive functions. As we have done in connection with quickSort, we write the running time of an invocation of a recursive function by T(n), where n denotes the size of the input. If n is of a particular form (for example, if n has a small value), then no recursive calls are made. Some fixed computation is done instead and the result is returned. In this case the techniques for non-recursive functions need be employed.
Finally, assume that the function makes recursive calls on inputs of sizes n1,n2,...,nk for some k>=1. Typically each ni is smaller than n. These calls take respective times T(n1),T(n2),...,T(nk). We add these times. Furthermore, we compute the time taken by the function without the recursive calls. Let us denote this time by g(n). We then have:
T(n) = T(n1) + T(n2) + ... + T(nk) + g(n).
Such an equation is called a recurrence relation. There are tools by which we can solve recurrence relations of some particular types. This is again part of the deadly combinatorics. We will not go to the details, but only mention that a recurrence relation for T(n) together with a set of initial conditions (e.g. T(n) for some small values of n) may determine a closed-form formula for T(n) which can be expressed by the Big O notation. It is often not necessary to compute an exact formula for T(n). Proving a lower and an upper bound may help us determine the order of T(n). Recall how we have analyzed the complexity of the recursive Fibonacci function.
We end this section with two other examples of complexity analysis of recursive functions.
Examples
- Computing determinants
The following function computes the determinant of an n x n matrix using the expand-at-the-first-row method. It recursively computes n determinants of (n-1) x (n-1) sub-matrices and then does some simple manipulation of these determinant values.
int determinant ( int A[SIZE][SIZE] , int n ) { int B[SIZE][SIZE], i, j, k, l, s; if (n == 1) return A[0][0]; s = 0; for (j=0; j<n; ++j) { for (i=1; i<n; ++i) { for (l=k=0; k<n; ++k) if (k != j) B[i-1][l++] = A[i][k]; } if (j % 2 == 0) s += A[0][j] * determinant(B,n-1); else s -= A[0][j] * determinant(B,n-1); } }I claim that this algorithm is an extremely poor choice for computing determinants. If T(n) denotes the running of the above function, we clearly have:
T(1) = 1, and T(n) >= n T(n-1) for n >= 2.
Multiple substitution of the second inequality then implies that:
T(n) >= n T(n-1) >= n(n-1) T(n-2) >= n(n-1)(n-2) T(n-3) ... >= n(n-1)(n-2)...2 T(1) = n!How big is n! (factorial n)? Since i >= 2 for i = 2,3,...,n, it follows that n! >= 2n-1. Thus the running-time of the above function is at least exponential.
Polynomial-time algorithms exist for computing determinants. One may use elementary row operations in order to reduce the given matrix to a triangular matrix having the same determinant. For a triangular matrix, the determinant is the product of the elements on the main diagonal. We urge the students to exploit this idea in order to design an O(n3) algorithm for computing determinants.
- Merge sort
The merge sort algorithm on an array of size n is depicted below:
void mergeSort ( int A[] , int n ) { if (n <= 1) return; mergeSort(A,n/2); mergeSort(&A[n/2],n-(n/2)); merge(A,0,n/2-1,n/2,n-1); }For simplicity, assume that n = 2t for some t. The merge step on two arrays of size n/2 can be easily seen to be doable in O(n) time. It then follows that:
T(1) = 1, and T(n) <= 2 T(n/2) + cn + d
for some constants c and d. As in the average case of quick sort, one can deduce the running time of merge sort to be O(nlog n).