Adder design

Ripple Carry Adder

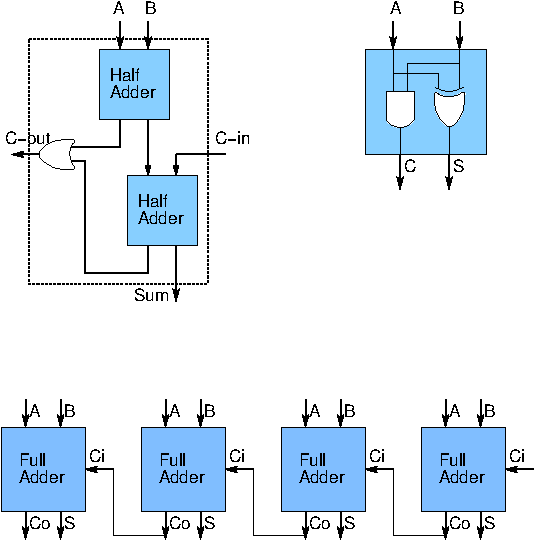
Half adder
A half adder is able to add two bits (say) A and B to product the sum S=A ⊕ B and the carry C=A · B.
Full adder
Addition of numbers also requires carries to be handled. Two half adders can be used to handle the two bits A and B along with the carry Ci, as indicated in the circuit, above. Now, sum S=A ⊕ B ⊕ Ci and the carry Co = (A · B) + Ci · (A ⊕ B) = (A · B) + Ci · (A + B)
RCA
When multi-bit words are to be added, the corresponding bits may be added pairwise and the carry can be rippled through to the next stage. With this scheme the time taken by the carry to ripple through n bits is proportional to n. While the circuit is simple, its delay is significant, making this schene unsuitable for adding number with several bits.
Adding faster with carry lookahead

Carry lookahead logic uses the concepts of generating and propagating carries. Although in the context of a carry lookahead adder, it is most natural to think of generating and propagating in the context of binary addition, the concepts can be used more generally than this. In the descriptions below, the word digit can be replaced by bit when referring to binary addition.

The addition of two 1-digit inputs A and B is said to generate if the addition will always carry, regardless of whether there is an input carry (equivalently, regardless of whether any less significant digits in the sum carry). For example, in the decimal addition 52 + 67, the addition of the tens digits 5 and 6 generates because the result carries to the hundreds digit regardless of whether the ones digit carries (in the example, the ones digit clearly does not carry).

In the case of binary addition, $A + B$ generates if and only if both A and B are 1. If we write $G (A, B)$ to represent the binary predicate that is true if and only if $A + B$ generates, we have:

G(A, B) = A · B

The addition of two 1-digit inputs A and B is said to propagate if the addition will carry whenever there is an input carry (equivalently, when the next less significant digit in the sum carries). For example, in the decimal addition 37 + 62, the addition of the tens digits 3 and 6 propagate because the result would carry to the hundreds digit if the ones were to carry (which in this example, it does not). Note that propagate and generate are defined with respect to a single digit of addition and do not depend on any other digits in the sum.

In the case of binary addition, $A + B$ propagates if and only if at least one of A or B is 1. If we write $P (A, B)$ to represent the binary predicate that is true if and only if $A + B$ propagates, we have:

$P (A, B) = A + B$

Sometimes a slightly different definition of propagate is used. By this definition A + B is said to propagate if the addition will carry whenever there is an input carry, but will not carry if there is no input carry. It turns out that the way in which generate and propagate bits are used by the carry lookahead logic, it doesn't matter which definition is used. In the case of binary addition, this definition is expressed by:

$P' (A, B) = A \oplus B$

For binary arithmetic, or is faster than xor and takes less transistors to implement, and therefore P(A,B) is usually used instead of P'(A,B). However, for a multiple-level carry lookahead adder, it is simpler to use P'(A,B)
Given these concepts of generate and propagate, when will a digit of addition carry? It will carry precisely when either the addition generates or the next less significant bit carries and the addition propagates. Written in boolean algebra, with C_i the carry bit of digit i, and P_i and G_i the propagate and generate bits of digit i respectively,
C_i+1 = G_i + (P_i · C_i)

Carry look ahead

C₁ = G₀ + (P₀ · C₀) = (A₀ · B₀) + C₀ · (A₀ + B₀) = A₀ · B₀ + C₀ · A₀ + C₀ · B₀
C₂ = G₁ + (P₁ · C₁) = (A₁ · B₁) + C₁ · (A₁ + B₁) = A₁ · B₁ + C₁ · A₁ + C₁ · B₁ =
A₁ · B₁ + (A₀ · B₀ · A₁ + C₀ · A₀ · A₁ + C₀ · B₀ · A₁) + (A₀ · B₀ · B₁ + C₀ · A₀ · B₁ + C₀ · B₀ · B₁)

It is evident that the size of the carry expression is increasing exponentially with the number of bits over which to carry; size(C_j) = 2 × size(C_j-1)+k; size(C₀)=0. This motivates the design of the block carry lookahead adder, where carry lookahead is peformed only over a few stages to avoid the blow up in the carry expression.
Limiting carry cost with Block Carry Lookahead Adder

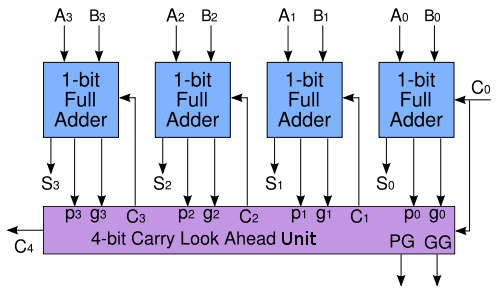
For each bit in a binary sequence to be added, the Carry Look Ahead Logic will determine whether that bit pair will generate a carry or propagate a carry. This allows the circuit to "pre-process" the two numbers being added to determine the carry ahead of time. Then, when the actual addition is performed, there is no delay from waiting for the ripple carry effect (or time it takes for the carry from the first Full Adder to be passed down to the last Full Adder). Below is a simple 4-bit generalized Carry Look Ahead circuit that combines with the 4-bit Ripple Carry Adder we used above with some slight adjustments:

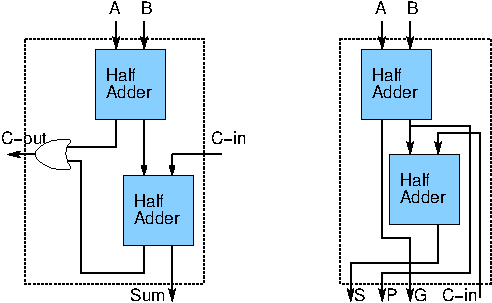
The schematics of a standard full adder (left) and a modified full adder (right) relevant for this assignment to be used here is given below:

For any circuit larger than 4 bits, the Carry Look Ahead circuitry becomes very complicated. For the example provided, the logic for the generate (g) and propagate (p) values are given below. Note that the numeric value determines the signal from the circuit above, starting from 0 on the far left to 3 on the far right:

C₁ = G₀ + P₀ · C₀

C₂ = G₁ + P₁ · C₁ = G₁ + P₁ · G₀ + P₁ · P₀ · C₀

C₃ = G₂ + P₂ · C₂ = G₂ + P₂ · G₁ + P₂ · P₁ · G₀ + P₂ · P₁ · P₀ · C₀

C₄ = G₃ + P₃ · C₃ = G₃ + P₃ · G₂ + P₃ · P₂ · G₁ + P₃ · P₂ · P₁ · G₀ + P₃ · P₂ · P₁ · P₀ · C₀

The cost of C_j, could be computed as follows: size(C_j) = k × (3 + j) + size(C_j-1); size(C₀)=0; this grows as the square of j.
The Block Carry Look Ahead 4-bit adder can also be used in a higher-level circuit by having each CLA Logic circuit produce a propagate and generate signal to a higher-level CLA Logic circuit. The group propagate ( $P G$ ) and group generate ( $G G$ ) for a 4-bit CLA are:

PG = P₀ · P₁ · P₂ · P₃

GG = G₃ + G₂ · P₃ + G₁ · P₃ · P₂ + G₀ · P₃ · P₂ · P₁

Putting four 4-bit CLAs together yields four group propagates and four group generates. A Lookahead Carry Unit (LCU) takes these eight values and uses identical logic to calculate $C i$ in the CLAs. The LCU then generates the carry input for each of the 4 CLAs and a fifth equal to $C 16$ .

Delay estimation

4-bit BCLA

Let Δ be a single gate delay
Delay to compute P_i/G_i=2Δ
Delay to compute C_i= Δ(for P_i/G_i)+ 2Δ(for 2-level SOP expression) = 3Δ
Delay to compute S_i= 3Δ(for C_i)+ 2Δ(for 2-level SOP expression) = 5Δ
Delay to compute PG/GG = 3Δ

16-bit BCLA

Delay to compute PG/GG = 3Δ
Delay to compute C_i for each block by top-level (bottom most) BCLA unit = 2Δ time
Delay to compute C_i for each FA after receiving the C_i into a block = 2Δ
Delay to compute S_i by FA = 7Δ(for C_i)+ 2Δ(for 2-level SOP expression) = 9Δ

64-bit BCLA

Compute the time for the block generate and propagate function from come to the top BCLA (bottom most) unit
Thereafter, compute the lookahead carries to be computed and ultimately C_i for each FA after receiving the C_i into a block
Finally determinie the delay to compute S_i by FA
An adder of 2^2k-bits will require 4-bit BCLA units at k levels
Delay = Δ (for PG/GG) + 2kΔ (downward computation for LA) + 2(k-1)Δ (upward computation for LA) + 2Δ = (4k+1)Δ ∈ O(k)
For 64-bits, k=3 and the delay is 13Δ

Cost estimation

On similar lines the overall cost of the adder built from the FA and BCLA units may also be estimated
An adder of 2^2k-bits will require that many 4-bit BCLA units at k levels
A FA for BCLA computes g=ab (cost=1) and a⊕b⊕C = ab'C'+a'bC'+a'b'C+abC (cost=14, including cost of complementation)
Overall cost of FA=15
For the BCLA, the costs are as follows:

C₁ cost = 2
C₂ cost = 5
C₃ cost = 9
C₄ cost = 14
PG cost = 3
GG cost = 9
Overall BCLA cost = 42

2^2k-bit cost = 15 × 2^2k + 42 × (2^2k-1)/3 ∈ O(2^2k) (linear in the number of bits)