Introduction
What is a digital computer?
A computer is a machine that can perform computation. It is difficult to give a precise definition of computation. Intuitively, a computation involves the following three components:
- Input: The user gives a set of input data.
- Processing: The input data is processed by a well-defined and finite sequence of steps.
- Output: Some data available from the processing step are output to the user.
Usually, computations are carried out to solve some meaningful and useful problems. One supplies some input instances for the problem, which are then analyzed in order to obtain the answers for the instances.
Types of problems
- Functional problems
A set of arguments a1,a2,...,an constitute the input. Some function f(a1,a2,...,an) of the arguments is calculated and output to the user.
- Decision problems
These form a special class of functional problems whose outputs are "yes" and "no" (or "true" and "false", or "1" and "0", etc).
- Search problems
Given an input object, one tries to locate some particular configuration pertaining to the object and outputs the located configuration, or "failure" if no configuration can be located.
- Optimization problems
Given an object, a configuration and a criterion for goodness, one finds and reports the configuration pertaining to the object, that is best with respect to the goodness criterion. If no such configuration is found, "failure" is to be reported.
Specific examples
- Polynomial root finding
Category: Functional problem
Input: A polynomial with real coefficients
Output: One (or all) real roots of the input polynomial
Processing: Usually, one involves a numerical method (like the Newton-Raphson method) for computing the real roots of a polynomial.- Matrix inversion
Category: Functional problem
Input: A square matrix with rational entries
Output: The inverse of the input matrix if it is invertible, or "failure"
Processing: Gaussian elimination is a widely used method for matrix inversion. Other techniques may also be conceived of.- Primality testing
Category: Decision problem
Input: A positive integer
Output: The decision whether the input integer is prime or not
Processing: For checking the primality of n, it is an obvious strategy to divide n by integers between 2 and square root of n. If a divisor of n is found, n is declared "composite" ("no"), else n is declared "prime" ("yes").This obvious strategy is, however, very slow. More practical primality testing algorithms are available. The first known (theoretically) fast algorithm is due to three Indians (Agarwal, Kayal and Saxena) from IIT Kanpur.
- Traveling salesman problem (TSP)
Category: Optimization problem
Input: A set of cities, the cost of traveling between each pair of cities, and the criterion of cost minimization
Output: A route through all the cities with each city visited only once and with the total cost of travel as small as possible
Processing: Since the total number of feasible routes for n cities is n!, a finite quantity, checking all routes to find the minimum is definitely a strategy to solve the TSP. However, n! grows very rapidly with n, and this brute-force search is impractical. We do not know efficient solutions for the TSP. One may, however, plan to remain happy with a suboptimal solution in which the total cost is not the smallest possible, but close to it.- Weather prediction
Category: Functional problem
Input: Records of weather for previous days and years. Possibly also data from satellites.
Output: Expected weather of Kharagpur for tomorrow
Processing: One statistically processes and analyzes the available data and makes an educated extrapolating guess for tomorrow's weather.- Web browsing
Category: Functional problem
Input: A URL (abbreviation for "Uniform Resource Locator" which is colloquially termed as "Internet site")
Output: Display (audio and visual) of the file at the given URL
Processing: Depending on the type of the file at the URL, one or more specific programs are run and the desired output is generated. For example, a web browser can render an HTML page, images in some formats etc. For displaying a movie, a separate software (or its plug-in) need be employed.- Chess : Can I win?
Category: Search problem
Input: A configuration of the standard 8x8 chess board and the player ("white" or "black") who is going to move next
Output: A winning move for the next player, if existent, or "failure"
Processing: In general, finding a winning chess move from a given state is a very difficult problem. The trouble is that one may have to explore an infinite number of possibilities. Even when the total possibilities are finite in number, that number is so big that one cannot expect to complete exploration of all of these possibilities in a reasonable time. A more practical strategy is to investigate all possible board sequences involving a small number of moves starting from the given configuration and to identify the best sequence under some criterion and finally prescribe the first move in the best sequence.
A computer is a device that can solve these and similar problems. A digital computer accepts, processes and outputs data in digitized forms (as opposed to analog forms).
- A computer is a fundamental discovery of human mind. It does not tend to mimic other natural phenomena (except perhaps our brain).
- A computer can solve many problems. This is in sharp contrast with most other engineering gadgets.
- Computers are programmable, i.e., one can solve one's own problems by a computer.
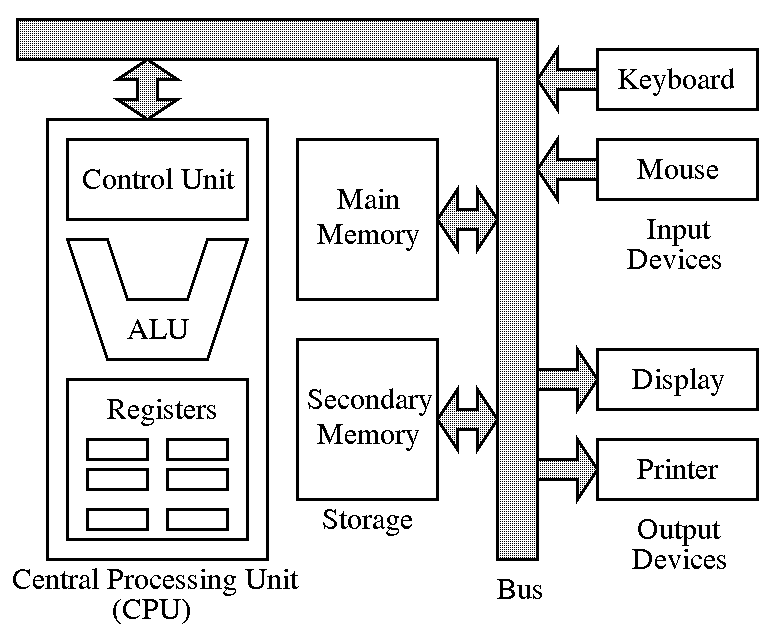
The basic components of a digital computer
In order that a digital computer can solve problems, it should be equipped with the following components:- Input devices
These are the devices using which the user provides input instances. In a programmable computer, input devices are also used to input programs. Examples: keyboard, mouse.
- Output devices
These devices notify the user about the outputs of a computation. Example: screen, printer.
- Processing unit
The central processing unit (CPU) is the brain of the computing device and performs the basic processing steps. A CPU typically consists of:
- An arithmetic and logical unit (ALU): This provides the basic operational units of the CPU. It is made up of units (like adders, multipliers) that perform arithmetic operations on integers and real numbers, and of units that perform logical operations (logical and bitwise AND, OR etc.).
- A control unit: This unit is responsible for controlling flow of data and instructions.
- General purpose registers: A CPU usually consists of a finite number of memory cells that work as scratch locations for storing intermediate results and values.
- External memory
The amount of memory (registers) resident in the CPU is typically very small and is inadequate to accommodate programs and data even of small sizes. Out-of-the-processor memory provides the desired storage space. External memory is classified into two categories:
- Main (or primary) memory: This is a high-speed memory that stays close to the CPU. Programs are first loaded in the main memory and then executed. Usually main memory is volatile, i.e., its contents are lost after power-down.
- Secondary memory: This is relatively inexpensive, bigger and low-speed memory. It is normally meant for off-line storage, i.e., storage of programs and data for future processing. One requires secondary storage to be permanent, i.e., its contents should last even after shut-down. Examples of secondary storage include floppy disks, hard disks and CDROM disks.
- Buses
A bus is a set of wires that connect the above components. Buses are responsible for movement of data from input devices, to output devices and from/to CPU and memory.
The interconnection diagram for a simple computer is shown in the figure below. This architecture is commonly called the John von Neumann architecture after its discoverer who was the first to give a concrete idea of stored program computers. Surprisingly enough, the idea of computation (together with a rich theory behind it) was proposed several decades earlier than the first real computer is manufactured. John von Neumann proposed the first usable draft of a working computer.
How does a program run in a computer?
The inputs, the intermediate values and the instructions defining the processing stage reside in the (main) memory. In order to separate data from instructions the memory is divided into two parts:
- Data area
The data area stores the variables needed for the processing stage. The values stored in the data area can be read, written and modified by the CPU. The data area is often divided into two parts: a stack part and a heap part. The stack part typically holds all statically allocated memory (global and local variables), whereas the heap part is used to allocate dynamic memory to programs during run-time.
- Instruction area
The instruction area stores a sequence of instructions that define the steps of the program. Under the control of a clock, the computer carries out a fetch-decode-execute cycle in which instructions are fetched one-by-one from the instruction area to the CPU, decoded in the control unit and executed in the ALU. The CPU understands only a specific set of instructions. The instructions stored in memory must conform to this specification.
The fetch-decode-execute cycle works as follows:
- For starting the execution of a program, a sequence of machine instructions is copied to the instruction area of the memory. Also some global variables and input parameters are copied to the data area of the memory.
- A particular control register, called the program counter (PC), is loaded with the address of the first instruction of the program.
- The CPU fetches the instruction from that location in the memory that is currently stored in the PC register.
- The instruction is decoded in the control unit of the CPU.
- The instruction may require one or more operands. An operand may be either a data or a memory address. A data may be either a constant (also called an immediate operand) or a value stored in the data area of the memory or a value stored in a register. Similarly, an address may be either immediate or a resident of the main memory or available in a register.
- An immediate operand is available from the instruction itself. The content of a register is also available at the time of the execution of the instruction. Finally, a variable value is fetched from the data part of the main memory.
- If the instruction is a data movement operation, the corresponding movement is performed. For example, a "load" instruction copies the data fetched from memory to a register, whereas a "save" instruction sends a value from a register to the data area of the memory.
- If the instruction is an arithmetic or logical instruction, it is executed in the ALU after all the operands are available in the CPU (in its registers). The output from the ALU is stored back in a register.
- If the instruction is a jump instruction, the instruction must contain a memory address to jump to. The program counter (PC) is loaded with this address. A jump may be conditional, i.e., the PC is loaded with the new address if and only if some condition(s) is/are true.
- If the instruction is not a jump instruction, the address stored in the PC is incremented by one.
- If the end of the program is not reached, the CPU goes to Step 3 and continues its fetch-decode-execute cycle.

Why need one program?
The electronic speed possessed by computers for processing data is really fabulous. Can you imagine a human prodigy manually multiplying two thousand digit integers flawlessly in an hour? A computer can perform that multiplication so fast that you even do not perceive that it has taken any time at all. It is wise to exploit this instrument to the best of our benefit. Why not, right?
However, there are many programs already written by professionals and amateurs. Why need we bother about writing programs ourselves? If we have to find roots of a polynomial or invert/multiply matrices or check primality of natural numbers, we can use standard mathematical packages and libraries. If we want to do web browsing, it is not a practical strategy that everyone writes his/her own browser. It is reported that playing chess with the computer could be a really exciting experience, even to world champions like Kasparov. Why should we write our own chess programs then? Thanks to the free (and open-source) software movement, many useful programs are now available in the public domain (often free of cost).
Still, we have to write programs ourselves! Here are some compelling reasons:
- There are so many problems to solve!
Simple counting arguments suggest that computers can solve infinitely many problems. Given that the age of the universe and the human population are finite, we cannot expect every problem to be solved by others. In other words, each of us is expected to encounter problems which are so private that nobody else has even bothered to solve them, let alone making the source-codes or executables freely available for our consumption. Sometimes programs are available for solving some of our problems, but these programs are either too costly to satisfy our budget or so privately solved by others that they don't want to share their programs with us. If we plan to harness the electronic speed of computers, there seems to be no alternative way other than writing the programs ourselves.
A stupendous example is provided by the proof of the four color conjecture, a curious mathematical problem that states that, given the map of any country, one can always color the states of the country using only four colors in such a way that no two states that share some boundary receive the same color. That five colors are sufficient was known long back, but the four color conjecture remained unsolved for quite a long time. Mathematicians reduced the problem to checking a list of configurations. But the list was so huge that nobody could even think of hand-calculating for all these instances. A computer program helped them explore all these possibilities. The four color conjecture finally came out to be true. Conservatives raised a huge hue and cry about such filthy methods of mathematical problem solving. But a problem solved happens to be a problem solved. Let the cynic cry!
Computers can aid you solving many problems of various flavors ranging from mundane to practical to esoteric to deeply theoretical. Moreover, anybody may benefit from programming computers, irrespective of his/her area of study. It's just your own sweet will whether you plan to exploit this powerful servant.
- Hey, we can write better programs than them!
Yes, we often can. Available programs may be too general and we can solve instances of our interest by specific programs much more efficiently than the general jack-of-all-trades stuff. Moreover, you may occasionally come up with brand-new algorithms that hold the promise of outperforming all previously known algorithms. You would then desire to program your algorithms to see how they perform in reality. Designing algorithms is (usually) a more difficult task than programming the algorithms, but the two may often go hand-in-hand before you jump to a practical conclusion.
How can one program?
Given a problem at hand, you tell the computer how to solve it and the machine does it. Unfortunately, telling the computer your processing steps is not that easy. Computers can be communicated with only in the language that they understand and are quite stubborn about that.
You have to specify the exact way in which the fetch-decode-execute cycle is to be carried out so that your problem is solved. The CPU of a computer supports a primitive set of instructions (typically, data movement, arithmetic, logical and jump instructions). Writing a program using these instructions (called assembly instructions) has two major drawbacks:
- The assembly language is so low-level that writing a program in this language is a very formidable task. One ends up with unmanageably huge codes that are very error-prone and extremely difficult to debug and update.
- The assembly language varies from machines to machines. The assembly codes suitable for one machine need not be understood by another machine. Moreover, different machines support different types of assembly instructions and there is no direct translation of instructions of one machine to those of another. For example, the ALU of Computer A may support integer multiplication, whereas that of Computer B does not. You have to translate each single multiplication instruction for Computer A to your own routine (say, involving additions and shifts) for doing multiplication in Computer B.
A high-level language helps you make your communication with computers more abstract and simpler and also widely machine-independent. You then require computer programs that convert your high-level description to the assembly-level descriptions of individual machines, one program for each kind of CPU. Such a translator is called a compiler.
Therefore, your problem solving with computers involves the following three steps:
- Write the program in a high-level language
You should use a text editor to key in your program. In the laboratory we instruct you to use the emacs editor. You should also save your program in a (named) file.
We are going to teach you the high-level language known as C.
- Compile your program
You need a compiler to do that. In the lab you should use the C compiler cc (a.k.a. gcc).
cc myprog.c
If your program compiles successfully, a file named a.out (an abbreviation of "assembler output") is created. This file stores the machine instructions that can be understood by the particular computer where you invoked the compiler.If compilation fails, you should check your source code. The reason of the failure is that you made one or more mistakes in specifying your idea. Compilers are very stubborn about the syntax of your code. Even a single mistake may let the compiler churn out many angry messages.
- Run the machine executable file
This is done by typing
./a.out
(and then hitting the return/enter button) at the command prompt.
Your first C programs
- The file intro1.c
This program takes no input, but outputs the string "Hello, world!"
in a line.
#include <stdio.h>
main ()
{
printf("Hello, world!\n");
}
- The file intro2.c
This program accepts an integer as input and outputs the same integer.
#include <stdio.h>
main ()
{
int n;
scanf("%d",&n);
printf("%d\n",n);
}
- The file intro3.c
This program takes an integer n as input and outputs its square
n2.
#include <stdio.h>
main ()
{
int n;
scanf("%d",&n);
printf("%d\n",n*n);
}
- The file intro4.c
This program takes an integer n as input and is intended to compute
its reciprocal 1/n.
#include <stdio.h>
main ()
{
int n;
scanf("%d",&n);
printf("%d\n",1/n);
}
Unfortunately, the program does not print the desired output. For input 0,
it prints "Floating exception". (Except for really esoteric situations,
division by 0 is a serious mathematical crime, so this was your punishment!)
For input 1 it outputs 1, whereas for input -1 it outputs -1. For any
other integer you input, the output is 0. That's too bad! But the accident
is illustrating. Though your program compiled gracefully and ran without
hiccups, it didn't perform what you intended. This is because you
made few mistakes in specifying your desire.
- The file intro5.c
A corrected version of the reciprocal printer is as follows:
#include <stdio.h>
main ()
{
int n;
scanf("%d",&n);
printf("%f\n",1.0/n);
}
For input 67 it prints 0.014925, for input -32 it prints -0.031250.
That's good work! However, it reports 1.0/0 as "Inf" (infinity).
Mathematicians may now turn very angry because you didn't get the
punishment you deserved.
This program takes no input, but outputs the string "Hello, world!" in a line.
#include <stdio.h>
main ()
{
printf("Hello, world!\n");
}
This program accepts an integer as input and outputs the same integer.
#include <stdio.h>
main ()
{
int n;
scanf("%d",&n);
printf("%d\n",n);
}
This program takes an integer n as input and outputs its square n2.
#include <stdio.h>
main ()
{
int n;
scanf("%d",&n);
printf("%d\n",n*n);
}
This program takes an integer n as input and is intended to compute its reciprocal 1/n.
#include <stdio.h>
main ()
{
int n;
scanf("%d",&n);
printf("%d\n",1/n);
}
Unfortunately, the program does not print the desired output. For input 0, it prints "Floating exception". (Except for really esoteric situations, division by 0 is a serious mathematical crime, so this was your punishment!) For input 1 it outputs 1, whereas for input -1 it outputs -1. For any other integer you input, the output is 0. That's too bad! But the accident is illustrating. Though your program compiled gracefully and ran without hiccups, it didn't perform what you intended. This is because you made few mistakes in specifying your desire.
A corrected version of the reciprocal printer is as follows:
#include <stdio.h>
main ()
{
int n;
scanf("%d",&n);
printf("%f\n",1.0/n);
}
For input 67 it prints 0.014925, for input -32 it prints -0.031250. That's good work! However, it reports 1.0/0 as "Inf" (infinity). Mathematicians may now turn very angry because you didn't get the punishment you deserved.