Pointers and dynamic memory allocation
All variables, arrays, structures and unions that we worked with so far are statically allocated, meaning that whenever an appropriate scope is entered (e.g. a function is invoked) an amount of memory dependent on the data types and sizes is allocated from the stack area of the memory. When the program goes out of the scope (e.g. when a function returns), this memory is returned back to the stack. There is an alternative way of allocating memory, more precisely, from the heap part of the memory. In this case, the user makes specific calls to capture some amount of memory and continues to hold that memory unless it is explicitly (i.e., by distinguished calls) returned back to the heap. Such memory is said to be dynamically allocated.
In order to exemplify the usefulness of dynamic memory allocation, suppose that there are two types of foomatic collections: the first type refers to an array of ten integers, whereas the second type refers to an array of ten million integers. A foomatic chain is made from a combination of one million collections of first type and few (say, ten) collections of the second type. Such a chain demands a total memory capable of holding 110 million integers. Assuming that an integer is of size 32 bits, this amounts to a memory of 440 Megabytes. A modern personal computer usually has enough memory to accommodate this data.
It is a foomatic convention to treat both types of collection uniformly, i.e., our plan is to represent both by a single data type. Think of the difference between you and me. I am the instructor (synonymously the president) of the class, whereas students are only listeners (synonymous with citizens). A president is the most important person in a society, he requires microphones, computers, bla bla bla. Still, both the president and each citizen are of the same data type called human.
So a foollection is a foomatic human capable of representing a collection of either type. If we plan to handle it using a structure with an array (or union), we must prepare for the bigger collections. The definition goes like this:
typedef struct {
int type;
int data[10000000];
} foollection;
Now irrespective of what a foollection data actually stores, it requires memory for ten million and one integers. (Think of each of you being given a PA system and a computer in the class.) A foomatic chain then requires over 40,000 Gigabytes of memory. This is sheer waste of space, since only 440 Megabytes suffice. Moreover, no personal computer I have heard of comes with so much memory including hard disks.
What is the way out? Let us plan to redefine foollection in the following way:
typedef struct {
int type;
int *data;
} foollection;
I have replaced the static array by a pointer. We will soon see that a pointer can be allocated memory from the heap and that the amount of memory to be allocated to each pointer can be specified during the execution of the program. Thus the data pointer in a foollection variable is assigned exactly as much memory as is needed. (It is as if when I come to the classroom, the run-time system gives me a PA system and a computer, whereas a student is given only a comfortable chair.) Now each collection requires, in addition to the actual data array, the space for an int variable and for a pointer, typically demanding 4 bytes each. So a foomatic chain requires a space overhead of slightly more than 8 Megabytes, i.e., a chain with all foomatic abstractions now fits in a memory of size less than 450 Megabytes. My computer has this much space.
Let me illustrate another situation where dynamic memory allocation proves to be extremely useful. Look at lists and trees made up of structures with self-referencing pointers:
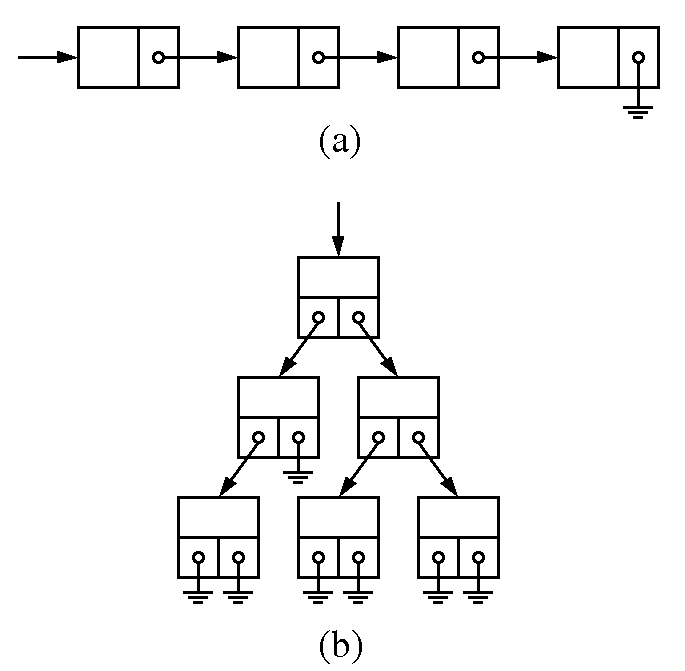
Figure: Dynamic lists
A static array can implement such lists, but has two disadvantages:
- The size of a static array is fixed during declaration, i.e., a static array can handle lists of a bounded size. Even if my machine has more memory than yours, I cannot leverage this superiority of my computer with static arrays. On the other extreme, irrespective of the actual size of the collection, a static array necessarily consumes the entire space for the biggest supportable collection.
- The linked structure can be incorporated in the framework of an array, but that requires (often awful) calculations to find the locations of the next objects. If pointers with dynamically assigned memory are used, accessing objects following the links becomes much easier.
So there is a big bunch of reasons why we should jump for dynamic memory management. Do it. But listen to the standard good advice from me. Dynamic memory allocation gives a programmer too much control of memory. Inexperienced programmers do not know how to effectively exploit that control. There remains every chance that everything gets repeatedly goofed up and the programmer, tired of fighting with segmentation faults for weeks, eventually gives up and joins the ice-cream industry. If you excel in this new job, I won't mind, even given that I am not a particular fan of ice-creams. But my job is to teach you programming, not how to manufacture tasty ice-creams.
One-dimensional dynamic memory
The built-in function malloc allocates a one-dimensional array to a pointer. You have to specify the total amount of memory (in bytes) that you would like to allocate to the pointer.
#define SIZE1 25 #define SIZE2 36 int *p; long double *q; p = (int *)malloc(SIZE1 * sizeof(int)); q = (long double *)malloc(SIZE2 * sizeof(long double));
The first call of malloc allocates to p a (dynamic) array capable of storing SIZE1 integers. The second call allocates an array of SIZE2 long double data to the pointer q. In addition to the size of each array, we need to specify the sizeof (size in bytes of) the underlying data type. malloc allocates memory in bytes and reads the amount of bytes needed from its sole argument.
If you demand more memory than is currently available in your system, malloc returns the NULL pointer. So checking the allocated pointer for NULLity is the way how one can check if the allocation request has been successfully processed by the memory management system.
malloc allocates raw memory from some place in the heap. No attempts are made to initialize that memory. It is the programmer's duty to initialize and then use the values stored at the locations of a dynamic array.
Animation example : 1-D dynamic memory |
Example: Let us now write a function that allocates an appropriate amount of memory to a foollection structure based on the type of the collection it is going to represent.
foollection initfc ( int type )
{
foollection fc;
/* Set type of the collection */
fc.type = type;
/* Allocate memory for the data pointer */
if (type == 1) fc.data = (int *)malloc(10*sizeof(int));
else if (type == 2) fc.data = (int *)malloc(10000000*sizeof(int));
else fc.data = NULL;
/* Check for error conditions */
if (fc.data == NULL)
fprintf(stderr, "Error: insufficient memory or unknown type.\n");
return fc;
}
Example: Let us now create a linked list of 4 nodes holding the integer values 3,5,7,9 from start to end. For simplicity we do not check for error conditions.
typedef struct _node {
int data;
struct _node *next;
} node;
node *head, *p;
int i;
head = (node *)malloc(sizeof(node)); /* Create the first node */
head->data = 3; /* Set data for the first node */
p = head; /* Next p will navigate down the list */
for (i=1; i<=3; ++i) {
p->next = (node *)malloc(sizeof(node)); /* Allocate the next node */
p = p->next; /* Advance p by one node */
p->data = 2*i+3; /* Set data */
}
p->next = NULL; /* Terminate the list by NULL */
An important thing to notice here is that we are always allocating memory to p->next and not to p itself. For example, first consider the allocation of head and subsequently an allocation of p assigned to head->next.
head = (node *)malloc(sizeof(node)); p = head->next; p = (node *)malloc(sizeof(node));
After the first assignment of p, both this pointer and the next pointer of *head point to the same location. However, they continue to remain different pointers. Therefore, the subsequent memory allocation of p changes p, whereas head->next remains unaffected. For maintaining the list structure we, on the other hand, want head->next to be allocated memory. So allocating the running pointer p is an error. One should allocate p->next with p assigned to head (not to head->next). Now p and head point to the same node and, therefore, both p->next and head->next refer to the same pointer -- the one to which we like to allocate memory in the subsequent step.
This example illustrates that the first node is to be treated separately from subsequent nodes. This is the reason why we often maintain a dummy node at the head and start the actual data list from the next node. We will see many examples of this convention later in this course.
There are two other ways by which memory can be allocated to pointers. The calloc call takes two arguments, a number n of cells and a size s of a data, and returns an allocated array capable of storing n objects each of size s. Moreover, the allocated memory is initialized to zero. If the allocation request fails, the NULL pointer is returned.
#define FOO_CHAIN_SIZE 1000000
typedef struct {
int type;
int *data;
} foollection;
foollection *foochain;
foochain = (foollection *)calloc(FOO_CHAIN_SIZE,sizeof(foollection));
This call creates an array of one million foollection structures (or NULL if the machine cannot provide the requested amount of memory). Each structure in the array is initialized to zero, i.e., each foochain[i].type is set to 0 and each foochain[i].data is set to NULL.
The realloc call reallocates memory to a pointer. It is essentially used to change the amount of memory allocated to some pointer. If the new size s' of the memory is larger than the older size s, then s bytes are copied from the old memory to the new memory. The remaining s'-s bytes are left uninitialized. On the contrary, if s'<s, then only s' bytes are copied. If the reallocation request fails, the original pointer remains unchanged and the NULL pointer is returned.
As an example, suppose that we want to change the size of the dynamic array pointed to by foochain from one million to two millions, but without altering the data currently stored in the array. We can use the following call:
#define NEW_SIZE 2000000
foochain = realloc(foochain, NEW_SIZE * sizeof(foollection));
if (foochain == NULL)
fprintf(stderr, "Error: unable to reallocate storage.\n");
Memory allocated by malloc, calloc or realloc can be returned to the heap by the free system call. It takes an allocated pointer as argument. For example, the foochain pointer can be deallocated memory by the call:
free(foochain);
When a program terminates, all allocated memory (static and dynamic) is returned to the system. There is no necessity to free memory explicitly. However, since memory is a bounded resource, allocating it several times, say, inside a loop, may eventually let the system run out of memory. So it is a good programming practice to free memory that will no longer be used in the program.
Two-dimensional dynamic memory
Allocating two-dimensional memory is fundamentally similar to allocating one-dimensional memory. One uses the same calls (malloc, etc.) described in the previous section. One should only be careful about the allocation sizes and the return types.
Recall that we have four ways of declaring two-dimensional arrays. These are summarized below:
#define ROWSIZE 100 #define COLSIZE 200 int A[ROWSIZE][COLSIZE]; int (*B)[COLSIZE]; int *C[ROWSIZE]; int **D;
The first array A is fully static. It cannot be allocated or deallocated memory dynamically. As the definition of A is encountered, the required amount of space is allocated to A from the stack area of the memory. When the definition of A expires (i.e., the scope of A ends, say, due to return from a function or exit from a block), the static memory is returned back to the stack. Each of the three other arrays (B,C,D) has a dynamic component in it. Let us study them case-by-case.
B is a pointer to an array of COLSIZE integers. So it can be allocated ROWSIZE rows in the following way:
B = (int (*)[COLSIZE])malloc(ROWSIZE * sizeof(int[COLSIZE]));
The same can be achieved in a more readable way as follows:
typedef int matrow[COLSIZE]; B = (matrow *)malloc(ROWSIZE * sizeof(matrow));
C is a static array of ROWSIZE int pointers. Therefore, C itself cannot be allocated or deallocated memory. The individual rows of C should be allocated memory.
int i;
for (i=0; i<ROWSIZE; ++i)
C[i] = (int *)malloc(COLSIZE * sizeof(int));
D is dynamic in both directions. First, it should be allocated memory to store ROWSIZE int pointers each meant for a row of the 2-D array. Each row pointer, in turn, should be allocated memory for COLSIZE int data.
int i;
D = (int **)malloc(ROWSIZE * sizeof(int *));
for (i=0; i<ROWSIZE; ++i)
D[i] = (int *)malloc(COLSIZE * sizeof(int));
The last two pointers C,D allow rows of different sizes, since each row is allocated memory individually.
That's all! It may be somewhat confusing to understand the differences among these four cases. Things become clearer once you realize what type of pointer each of A,B,C,D is.
Animation example : 2-D dynamic memory |
Though the internal organizations of these arrays are quite different in the memory, their access mechanism is the same in the sense that the same notation Array_name[i][j] refers to the i,j-th entry in each of the four arrays. In order to promote this uniformity, the C compiler has to be quite fussy about the types of these arrays. Typecasting among these four types is often a crime that may result in mild warnings to failure of compilation to segmentation faults. Take sufficient care. Beware of the ice-cream industry!
The freeing mechanism is also different for the four arrays.
int i; /* A is a static array and cannot be free'd */ /* B is a single pointer */ free(B); /* C is a static array of pointers each to be free'd individually */ for (i=0; i<ROWSIZE; ++i) free(C[i]); /* Free each row */ /* D is a pointer to pointers. Each of these pointers is to be free'd */ for (i=0; i<ROWSIZE; ++i) free(D[i]); /* Free each row */ free(D); /* Free the row top */
I think it suffices to learn to work with only the completely static (A) and the completely dynamic (D) versions of 2-D arrays. They are my personal favorites and any-time recommendations.
Still, if you care, here follows a program that shows you the internal organizations of each memory cell and each row header for these four kinds of arrays. The addresses are displayed as byte distances relative to the header of the entire matrix.
#include <stdio.h>
#define ROWSIZE 4
#define COLSIZE 5
int A[ROWSIZE][COLSIZE];
int (*B)[COLSIZE];
int *C[ROWSIZE];
int **D;
int main ()
{
int i, j;
printf("\nArray A\n");
printf("sizeof(*A) = %d\n",sizeof(*A));
printf(" j=0 j=1 j=2 j=3 j=4\n");
printf(" +-------------------------------+\n");
for (i=0; i<ROWSIZE; ++i) {
printf("A[%d] = %4d : i=%d |", i, (int)A[i]-(int)A, i);
for (j=0; j<COLSIZE; ++j)
printf("%6d", (int)(&A[i][j])-(int)A);
printf(" |\n");
}
printf(" +-------------------------------+\n");
printf("\nArray B\n");
B = (int (*)[COLSIZE])malloc(ROWSIZE * sizeof(int[COLSIZE]));
printf("sizeof(*B) = %d\n",sizeof(*B));
printf(" j=0 j=1 j=2 j=3 j=4\n");
printf(" +-------------------------------+\n");
for (i=0; i<ROWSIZE; ++i) {
printf("B[%d] = %4d : i=%d |", i, (int)B[i]-(int)B, i);
for (j=0; j<COLSIZE; ++j)
printf("%6d", (int)(&B[i][j])-(int)B);
printf(" |\n");
}
printf(" +-------------------------------+\n");
printf("\nArray C\n");
for (i=0; i<ROWSIZE; ++i)
C[i] = (int *)malloc(COLSIZE * sizeof(int));
printf("sizeof(*C) = %d\n",sizeof(*C));
printf(" j=0 j=1 j=2 j=3 j=4\n");
printf(" +-------------------------------+\n");
for (i=0; i<ROWSIZE; ++i) {
printf("C[%d] = %4d : i=%d |", i, (int)C[i]-(int)C, i);
for (j=0; j<COLSIZE; ++j)
printf("%6d", (int)(&C[i][j])-(int)C);
printf(" |\n");
}
printf(" +-------------------------------+\n");
printf("\nArray D\n");
D = (int **)malloc(ROWSIZE * sizeof(int *));
for (i=0; i<ROWSIZE; ++i)
D[i] = (int *)malloc(COLSIZE * sizeof(int));
printf("sizeof(*D) = %d\n",sizeof(*D));
printf(" j=0 j=1 j=2 j=3 j=4\n");
printf(" +-------------------------------+\n");
for (i=0; i<ROWSIZE; ++i) {
printf("D[%d] = %4d : i=%d |", i, (int)D[i]-(int)D, i);
for (j=0; j<COLSIZE; ++j)
printf("%6d", (int)(&D[i][j])-(int)D);
printf(" |\n");
}
printf(" +-------------------------------+\n");
}
A sample output of this program executed in my machine follows:
Array A
sizeof(*A) = 20
j=0 j=1 j=2 j=3 j=4
+-------------------------------+
A[0] = 0 : i=0 | 0 4 8 12 16 |
A[1] = 20 : i=1 | 20 24 28 32 36 |
A[2] = 40 : i=2 | 40 44 48 52 56 |
A[3] = 60 : i=3 | 60 64 68 72 76 |
+-------------------------------+
Array B
sizeof(*B) = 20
j=0 j=1 j=2 j=3 j=4
+-------------------------------+
B[0] = 0 : i=0 | 0 4 8 12 16 |
B[1] = 20 : i=1 | 20 24 28 32 36 |
B[2] = 40 : i=2 | 40 44 48 52 56 |
B[3] = 60 : i=3 | 60 64 68 72 76 |
+-------------------------------+
Array C
sizeof(*C) = 4
j=0 j=1 j=2 j=3 j=4
+-------------------------------+
C[0] = 1004 : i=0 | 1004 1008 1012 1016 1020 |
C[1] = 1028 : i=1 | 1028 1032 1036 1040 1044 |
C[2] = 1052 : i=2 | 1052 1056 1060 1064 1068 |
C[3] = 1076 : i=3 | 1076 1080 1084 1088 1092 |
+-------------------------------+
Array D
sizeof(*D) = 4
j=0 j=1 j=2 j=3 j=4
+-------------------------------+
D[0] = 24 : i=0 | 24 28 32 36 40 |
D[1] = 48 : i=1 | 48 52 56 60 64 |
D[2] = 72 : i=2 | 72 76 80 84 88 |
D[3] = 96 : i=3 | 96 100 104 108 112 |
+-------------------------------+