Arrays
We have already discussed how one can define and initialize arrays and access individual cells of an array. In this chapter we introduce some advanced techniques related to handling of arrays.
Passing arrays to functions
We have seen how individual values (variables and pointers) can be passed to functions. Now let us see how we can pass an entire array to a function.
Suppose an array is defined as:
#define MAXSIZE 100 int myarr[MAXSIZE];
In order to pass the array myarr to a function foonction one may define the function as:
int foonction ( int A[MAXSIZE] , int size )
{
...
}
This function takes two arguments, the first is an array of size MAXSIZE, and the second an integer argument named size. Here this second argument is meant for passing the actual size of the array. Your array can hold 100 integers. However, at a certain point of time you may be using only 32 locations (0 through 31) of the array. The other unused locations also hold some values. If they are not initialized, they contain unpredictable values. You do not want these garbage values to be interpreted by your function as important ones. So you specify the actual size to be 32. The function call should go like this:
foonction(myarr,32);
Inside the function the array location myarr[i] can be accessed (read or written) as A[i]. It is very important to note that:
When you pass an array to a function, all changes you make in the array locations are visible from outside. |
In this example setting A[5] to 20 inside the function also changes myarr[5] to 20. This apparently contradicts the pass-by-value call mechanism of C. But the actual scenario is not so. When you pass an array, the entire array is not copied element-by-element. What is copied is the address of the first (I mean, the zeroth) location of the array. That is indeed a pointer. This dual meaning of an array will be dealt with at length later in this chapter.
You don't have to specify the length of the array in the function declaration. This is again because the array is not copied element-wise. Only the starting address of the array is passed. The function call does not allocate memory for the elements of the array. Therefore, it does not matter how big the array is. However, it is necessary to mention that the argument that is passed is an array and not an element of the constituent data type. The following declaration is adequate and admissible:
int foonction ( int A[] , int size )
{
...
}
Animation example : passing arrays to functions | Interactive animation : passing arrays to functions |
Strings
In C a string is defined to be a null-terminated character array. The null character ('\0') is used to indicate the end of the string. Like any other arrays, C does not impose range checking of array indices for strings. Declaration of an array allocates a fixed space for it. You need not use the entire space. Instead you can store your data in the initial portion of the array. It is, therefore, necessary to put a boundary of the actual data. This is the reason why we passed the size parameter to foonction above. Strings handle it differently, namely by putting an explicit marker at the end of the actual data. Here is an example of a string:
| I | I | T | K | h | a | r | a | g | p | u | r | , | 7 | 2 | 1 | 3 | 0 | 2 | \0 | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
Here we use an array of size 30. The string "IIT Kharagpur, 721302" is stored in the first 21 locations. This is followed by the null character. A total of 22 characters is needed to represent this string of length 21. Whatever follows after this null character is irrelevant for defining the string. If we set the element at location 6 to '\0', the array looks like:
| I | I | T | K | h | \0 | r | a | g | p | u | r | , | 7 | 2 | 1 | 3 | 0 | 2 | \0 | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
Considered as a string this stands for "IIT Kh".
Recall that C allows you to read from and write to the locations at indices 30,31,... of this array. These are memory locations not allocated to the array, since its size is 30. Writing beyond the allocated space is expected to corrupt memory or even raise fatal run-time errors (Segmentation faults). In particular, if you do not put the null character at the end of the string, C keeps on searching for it and may go out of the legal boundary and create troubles.
C offers some built-in functions for working with strings. They assume (null-terminated) strings as input and create (null-terminated) strings. You do not have to append the null character explicitly. For example, the statement
strcpy(A,"IIT Kharagpur");copies the string "IIT Kharagpur" to the character array A and also appends the required null character at the end of it.
In order to use these string functions you should #include <string.h>. No additional libraries need be linked during compilation time. The math library was quite different. Well, mathematics and mathematicians are traditionally known to be different from the rest of the lot!
- int strlen (const char s[]);
- Returns the length (the number of characters before the first null character) of the string s.
- int strcmp (const char s[], const char t[]);
- Compares strings s and t. Returns 0 if the two strings are identical, a negative value if s is lexicographically smaller than t (i.e., if s comes before t in the standard dictionary order), and a positive value if s is lexicographically larger than t.
- int strncmp (const char s[], const char t[], size_t n);
- Compares the prefixes of strings s and t of length n. Returns 0, a negative value or a positive value according as whether the prefix of s is equal to, lexicographically smaller than or lexicographically larger than the prefix of t. If a string (s or t) is already of length l < n, then the first l characters of the string (i.e., the entire string) is considered for the comparison. The decision of strncmp is based on the relative placement of the prefixes according to dictionary rules. For example, the string "IIT" comes before "MIT", "UIUC" and "IITian", but comes after "IIIT", "BITS" and "I" in the standard dictionary order. Note that string comparison is done in a case-sensitive manner. 'A' has the ASCII value (65) less than that for 'a' (95) and so 'A' comes before 'a' in the lexicographic order. It is more correct to say that comparison is done with respect to ASCII values, whereas ASCII values are assigned to characters based broadly on the dictionary order. Case-sensitivity is inherent in ASCII. You have to live with it.
- char *strcpy (char s[], const char t[]);
- Copies the string t to the string s.
- char *strncpy (char s[], const char t[] , size_t n);
- Copies the prefix of t of size n to s. Again if t is of size l < n, then only l characters are copied to s. In all these cases a trailing null character is also copied to s.
- char *strcat (char s[], const char t[]);
- Appends the string t and then the null character at the end of s. The string s (a pointer, see below) is returned.
- char *strncat (char s[], const char t[], size_t n);
- Appends the first n characters of t and then the null character at the end of s. If t is of length l < n, then only l characters of t are appended to s. The string s is returned.
- int *strchr (const char s[], int c);
- Returns the pointer to the first occurrence of the integer c (treated as a character under the ASCII encoding). If the character c does not occur in s, the NULL pointer is returned.
- int *strrchr (const char s[], int c);
- Returns the pointer to the last occurrence of the integer c (treated as a character under the ASCII encoding). If the character c does not occur in s, the NULL pointer is returned.
Arrays and pointers
The double entendre of arrays constitutes a confusing and yet beautiful feature of C. An array is an array, if it is viewed so. One can access elements by the usual square bracket notation (like A[i]). In addition, an array A is also a pointer. You can assign pointers of similar types to A and do pointer arithmetic in order to navigate through the elements of the array.
Consider an array of integers and an int pointer:
#define MAXSIZE 10 int A[MAXSIZE], *p;
The following are legal assignments for the pointer p:
p = A; /* Let p point to the 0-th location of the array A */ p = &A[0]; /* Let p point to the 0-th location of the array A */ p = &A[1]; /* Let p point to the 1-st location of the array A */ p = &A[i]; /* Let p point to the i-th location of the array A */
Whenever p is assigned the value &A[i], the value *p refers to the array element A[i], and so also does p[0].
Pointers can be incremented and decremented by integral values. After the assignment p = &A[i]; the increment p++ (or ++p) lets p one element down the array, whereas the decrement p-- (or --p) lets p move by one element up the array. (Here "up" means one index less, and "down" means one index more.) Similarly, incrementing or decrementing p by an integer value n lets p move forward or backward in the array by n locations. Consider the following sequence of pointer arithmetic:
p = A; /* Let p point to the 0-th location of the array A */ p++; /* Now p points to the 1-st location of A */ p = p + 6; /* Now p points to the 7-th location of A */ p += 2; /* Now p points to the 9-th location of A */ --p; /* Now p points to the 8-th location of A */ p -= 5; /* Now p points to the 3-rd location of A */ p -= 5; /* Now p points to the (-2)-nd location of A */
Oops! What is a negative location in an array? Like always, C is pretty liberal in not securing its array boundaries. As you may jump ahead of the position with the largest legal index, you are also allowed to jump before the opening index (0). Though C allows you to do so, your run-time memory management system may be unhappy with your unhealthy intrusion and may cause your program to have a premature termination (with the error message "Segmentation fault"). It is the programmer's duty to insure that his/her pointers do not roam around in prohibited areas.
Here is an example of a function that computes the sum of the elements of an array. The naive method for doing so is:
int fooddition1 ( int A[] , int size )
{
int i;
int sum = 0;
for (i=0; i<size; ++i) sum += A[i];
return (sum);
}
The second method uses pointers:
int fooddition2 ( int A[] , int size )
{
int i, *p;
int sum = 0;
p = A; /* Let p point to the 0-th location of A */
for (i=0; i<size; ++i) {
sum += *p; /* Add to sum the element pointed to by p */
++p; /* Let p point to the next location in A */
}
return (sum);
}
Here is a third method that uses pointers in a subtler way:
int fooddition3 ( int A[] , int size )
{
int i, *p;
int sum = 0;
p = A;
for (i=0; i<size; ++i) sum += *(p + i);
return (sum);
}
Some key points need be highlighted now.
- Pointers are addresses in memory. If that is so, it apparently does not matter whether it is a pointer to an int or a char or a double etc. But the pointer arithmetic brings out the difference. Different data types require different amounts of space. For example, an int typically requires 4 bytes, a char only one byte, a double eight bytes, and so on. Now when you talk about the pointer p+i, the actual memory address depends on how much (in bytes) one needs to advance p in order to generate the i-th address. The amount of advance is dependent on the data type that the pointer points to. For int pointers, p+i refers to 4i bytes ahead in memory. For char pointers, this is just i bytes ahead of p. Finally, for double pointers, p+i is 8i bytes ahead of p. The notation p+i is an abstraction that hides the details of organization of data in the memory. You don't have to remember how much space each data type requires. C will automatically advance your pointers by appropriate amounts.
- Arrays and pointers are almost the same, but not identical. You
can assign addresses to pointers. But you are not allowed to do the same on
arrays. An array can only be declared, but cannot be assigned. Only the
elements of an array can be assigned values. For example, if we declare:
int A[MAXSIZE];
the following are not legal assignments:A = &(A[2]); ++A;
However, statements like
p = A + i; sum += *(A + i);
are permitted, because they do not involve assignment of A.
- In a function declaration (or prototype) where an array need be
passed, we can pass a pointer instead. We have mentioned earlier that
passing arrays to a function does not copy the array element-by-element.
It only passes the address of the (0-th entry of the) array. We can
substitute that by an explicit pointer. Here is how we can rewrite the
fooddition routine.
int fooddition4 ( int *A , int size ) { int i = 0, sum = 0; while (i < size) { sum += *A; ++A; ++i; } return (sum); } int main () { int A[5] = {3, 5, 7, 11, 13}; int s; /* Compute the sum of all five elements of A */ s = fooddition4(A,5); /* Compute the sum of the first through third elements of A */ s = fooddition4(&A[1],3); }The formal parameter A in fooddition4 is a pointer. It can be incremented (like ++A;). On the other hand, A refers to an array in main and so an increment like ++A; is not allowed in main.
Multi-dimensional arrays
One-dimensional arrays are quite able to represent many natural collections. There are some other natural collections that may better be conceptualized as 2-dimensional data. The first example is a matrix. What else can be a more natural 2-dimensional data other than a matrix whose entries are natural numbers? So think of the following 4x5 matrix:
1 1 1 1 1 2 3 4 5 6 4 9 16 25 36 8 27 64 125 216
We can write the entries in the row-major order and represent the resulting flattened data as a one-dimensional array:
1 1 1 1 1 2 3 4 5 6 4 9 16 25 36 8 27 64 125 216
As long as the column dimension of the matrix is known, the original matrix can be recovered easily from this 1-D array. More precisely, consider an m-by-n matrix (a matrix with m rows and n columns). It contains a total of mn elements. Let us number the rows 0,1,...,m-1 from top to bottom and the columns 0,1,...,n-1 from left to right. The entry at position (i,j) then maps to the (ni+j)-th entry of the one-dimensional array. On the other hand, the k-th entry of the one-dimensional array corresponds to the (i,j)-th element of the matrix, where i = k / n and j = k % n.
One-dimensional arrays suffice. Still, it is convenient and intuitive to visualize matrices as two-dimensional arrays. C provides constructs to define and work with such arrays. Of course, the memory of a computer is typically treated as a one-dimensional list of memory cells. Any two-dimensional structure has to be flattened using a strategy like that mentioned above. C handles this for you. In other words, the abstraction relieves you from the task of doing the index arithmetic explicitly. You refer to the (i,j)-th element as the (i,j)-th element. C translates it into the appropriate address in the one-dimensional memory.
2-dimensional arrays can be defined like one-dimensional arrays, but with two square-bracketed dimensions. For example, the declaration
int matrix[20][10];
allocates memory for a 20x10 array of int variables. The first index (20) indicates the number of rows allocated, whereas the second indicates the number of columns allocated. Here is another example:
#define MAXROW 50 #define MAXCOL 50 float M[MAXROW][MAXCOL];
Elements of a 2-D array can be initialized to constant values using nested curly braces:
int mat[4][5] =
{
{ 1, 1, 1, 1, 1 }, /* The zeroth row */
{ 2, 3, 4, 5, 6 }, /* The first row */
{ 4, 9, 16, 15, 25 }, /* The second row */
{ 8, 27, 64, 125, 216 } /* The third row */
};
Rows of a 2-D array of characters can be initialized to constant strings.
char address[4][100] = {
"Department of Foobarnautic Engineering",
"Indian Institute of Technology",
"Kharagpur 721302",
"India"
};
For a 2-D array A the (i,j)-th element is treated as a variable and can be accessed by the name A[i][j]. Both the row numbering and the column numbering start from 0. For example, the (1,3)-th element of mat is accessed as mat[1][3] and, if initialized as above, stores the int value 5.
Animation example : in-place transpose of a matrix |
2-D arrays can be passed to functions using a syntax similar to the declaration of 2-D arrays:
#define ROWDIM 10
#define COLDIM 12
int fooray ( int A[ROWDIM][COLDIM], int r , int c )
{
...
}
Here the actual row and column dimensions of the used part of the array A are passed via the parameters r and c. It is not mandatory to specify the row dimension ROWDIM. But the column dimension COLDIM must be specified, since 2-D to 1-D mapping in memory requires the column dimension. Thus the declaration
int fooray ( int A[][COLDIM], int r , int c )
{
...
}
is allowed, whereas the declarations
int fooray ( int A[][], int r , int c )
{
...
}
and
int fooray ( int A[ROWDIM][], int r , int c )
{
...
}
are not allowed.
Like 1-D arrays, 2-D arrays are not copied element-by-element to functions. A pointer is only passed. This implies that changes made to the array elements inside the function are visible outside the function.
Indeed 2-D arrays are pointers too. However, these pointers are rather distinct in nature from those pointers that represent 1-D arrays. The situation is quite clumsy and confusing.
#define MAXROW 4
#define MAXCOL 5
int barsum ( int A[][MAXCOL] , int r , int c )
{
int i, j, s;
int (*p)[MAXCOL];
s = 0;
p = A;
for (i=0; i<r; ++i) for (j=0; j<c; ++j) s += p[i][j];
return s;
}
The array A[][MAXCOL] can be assigned to the pointer p that should be declared as:
int (*p)[MAXCOL];
This declaration means that p is a pointer to an array of MAXCOL integers. The parentheses surrounding *p are absolutely necessary for this. The declaration
int *p[MAXCOL];
won't work in this context. The reason is that the array indicator [] has higher precedence than the pointer indicator *. Therefore, the last declaration is equivalent to
int *(p[MAXCOL]);
and means that p is an array of MAXCOL int pointers. This does not match the type of A. In addition, this does not match the dimension of A.
There are four ways in which a 2-D array may be declared.
#define MAXROW 4 #define MAXCOL 5 int A[MAXROW][MAXCOL]; /* A is a statically allocated array */ int (*B)[MAXCOL]; /* B is a pointer to an array of MAXCOL integers */ int *C[MAXROW]; /* C is an array of MAXROW int pointers */ int **D; /* D is a pointer to an int pointer */
All these are essentially different in terms of memory management. Except the first array A, the three other arrays support dynamic memory allocation. When properly allocated memory, each of these can be used to represent a MAXROW-by-MAXCOL array. Moreover, in all the four cases the (i,j)-th entry of the array is accessed as Array_name[i][j]. The first two (A and B) are pointers to arrays, whereas the last two (C and D) are arrays of pointers. The following figure elaborates this difference.
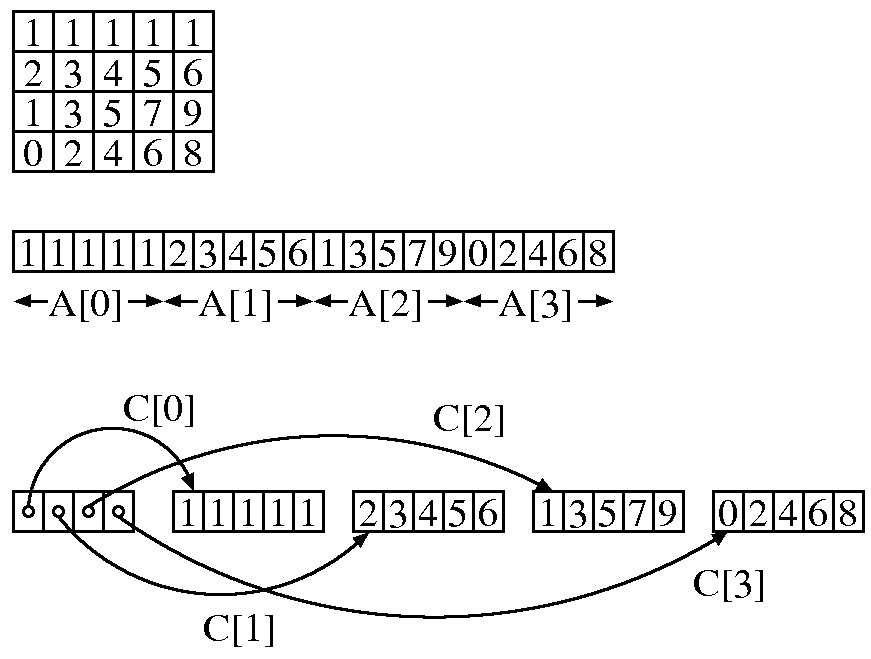
Figure: Two-dimensional arrays
We will discuss more about two-dimensional arrays in the chapter on dynamic memory allocation.