Graceful Spheres

CAUTION! This webpage has SVG images and your browser does not support it.

Algorithm

Ranita Biswas, Partha Bhowmick, and Valentin E. Brimkov,
On the Polyhedra of Graceful Spheres and Circular Geodesics,
Discrete Applied Mathematics, Vol. 216, pp. 362-375, 2017.

Contribution

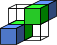
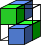
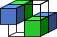
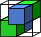
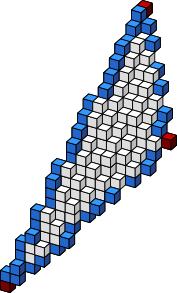
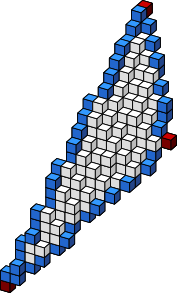
We construct a polyhedral surface called a graceful surface, which provides best possible approximation to a given sphere regarding certain criteria. In digital geometry terms, the graceful surface is uniquely characterized by its minimality while guaranteeing the connectivity of certain discrete (polyhedral) curves defined on it. The notion of gracefulness was first proposed by Brimkov and Barneva in Graceful planes and lines (Theoretical Computer Science, 283:151-170, 2002) and shown to be useful for triangular mesh discretization through graceful planes and graceful lines. In this paper we extend the considerations to a nonlinear object such as a sphere. In particular, we investigate the properties of a discrete geodesic path between two voxels and show that discrete 3D circles, circular arcs, and Mobius triangles are all constructible on a graceful sphere, with guaranteed minimum thickness and the desired connectivity in the discrete topological space.
Figure on right: A graceful sphere for r=15. Voxels comprising the naive sphere are shown in white, and the Steiner voxels in color. Yellow, green, and blue are for three different functional planes, and violet indicates two or more functional planes for the same Steiner voxel.

Tandem configurations
xy
1, 2, 43, 44
7, 8, 37, 38
13, 14, 31, 32
19, 20, 25, 26
yz
3, 4, 45, 46
9, 10, 39, 40
15, 16, 33, 34
21, 22, 27, 28
zx
5, 6, 47, 48
11, 12, 41, 42
17, 18, 35, 36
23, 24, 29, 30
Figure on left: Tandem configurations appearing on 48 q-octants, as shown below the respective configurations. Configurations with the same functional plane are shown in a row. The two voxels comprising a jump are shown in blue, and the other two voxels of naive sphere are shown hollow. The two voxels shown in green are Steiner voxels, and a graceful geodesic path would include at most one of them.

Mobius triangles

The graceful sphere is the thinnest possible discrete sphere for which, in the framework of generation scheme, Euclidean primitives like geodesic paths, geodesic circles, and Mobius/spherical triangles (as well as arbitrary spherical polygons) are always well-connected sets of voxels. The connectivity of an edge (3D geodesic or circular arc) of a Mobius triangle is not guaranteed when defined on a naive sphere, which is however ensured when the edges are taken from the corresponding graceful sphere.
Figure on right: Comparison among different types of Mobius triangle. For each type in this example, the vertices (shown in red) are (7,2,29), (12,24,13), (18,15,19) and belong to the naive sphere of radius 30; the interior of the triangle is a subset of the naive sphere, and its sides are naive, graceful, and standard (left to right).