Assignment No 6
Binary Search Trees with Duplicate Key Values
In this exercise, we add a provision to allow a BST to store the same key value multiple times. For example, the BST could store students records, and the ordering is with respect to CGPA. If multiple students have the same CGPA, then the BST can now store the records of all these students simultaneously. In order to do this, we have to change the definition of a BST slightly. For any node u, we will now have:
| Values at all nodes in the left subtree of u < Value at u ≤ Values at all nodes in the right subtree of u |
This means that we always push repeated values to the right subtree of a current occurrence. An example of a BST with repeated values is shown in the figure below.
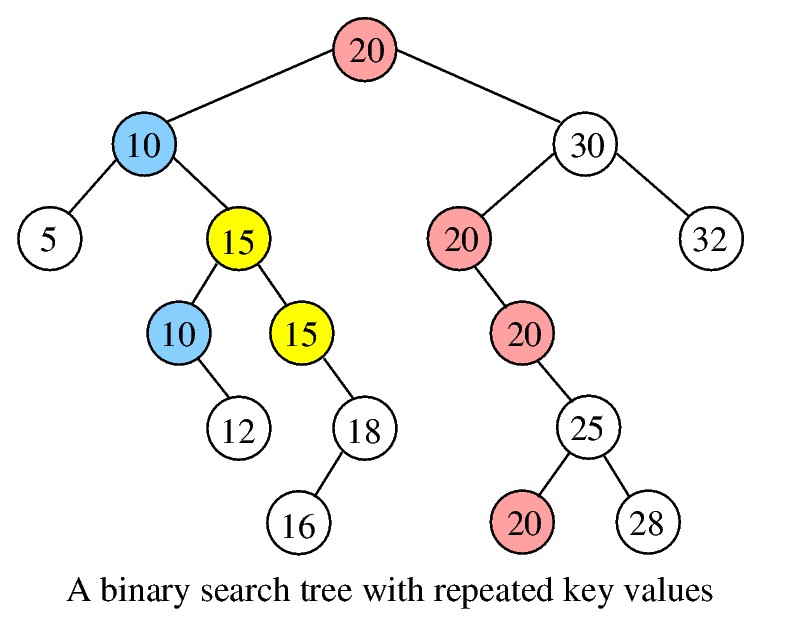
Implement the following functions on a BST T supporting duplicate entries. Assume that each node in the tree contains only a key value and two child pointers (and nothing else like parent pointers or any other information). We will let n be the number of nodes in T, and h the height of T.
- Search(T,x): This function should return the count of occurrences of x in T. The return value 0 means that x is not present in T. This function must run in O(h) time, independent of the number of occurrences of x in T.
- Insert(T,x): Irrespective of how many instances of x are already present in the tree, this function will insert a fresh occurrence of x in T. The standard BST insertion routine is followed with the only exception that the detection of the presence of x would not break the search loop. The loop will instead reach a suitable node q, and the new key value is inserted as a suitable child of q. At this point, the new inserted node must be a leaf in T. This function should also run in O(h) time.
- Delete(T,x): This function should delete all occurrences of x from T in a total of O(h) time. The function would first locate the topmost occurrence of x in T. If no such occurrence can be found, there is nothing to be done. Otherwise, the function will remember (a pointer to) this topmost occurrence. It will then make a single downward pass in order to delete all the remaining occurrences of x. By construction, all these occurrences lie in different levels, and have their left subtrees empty. So deleting the duplicate entries is easy (O(1) time per node). After the duplicate entries are removed, the function deletes the topmost occurrence (the only occurrence left now) as in the standard BST deletion procedure.
- Inorder traversal of T: This gives a sorted listing of the key values stored in T. If repeated values are stored, it should also print the occurrence number. the occurrence number is not stored in the nodes of the tree. By passing suitable parameters to the traversal function, this printing can be managed.
- The main() function: Read the number n of entries and a maximum value m of each entry. Insert, in an initially empty BST, n random integers each in the range 1 through m, using the insert function. After n integers are inserted, the inorder traversal of the tree will print the values stored in T. Then, make a few (like ten to twenty) random searches in the tree. Finally, delete randomly chosen values from T a few times (like five to ten times). For searching and deletion, the random values may be generated in the range 1 through m. Make the inorder listing of the tree after each deletion.
Sample Output
n = 40
m = 20
+++ Inserting 40 random integers between 1 and 20
1 (1) 1 (2) 1 (3) 1 (4) 2 (1) 3 (1) 3 (2) 3 (3)
4 (1) 4 (2) 5 (1) 5 (2) 5 (3) 5 (4) 7 (1) 8 (1)
8 (2) 9 (1) 9 (2) 9 (3) 9 (4) 9 (5) 10 (1) 11 (1)
11 (2) 11 (3) 12 (1) 13 (1) 13 (2) 14 (1) 16 (1) 16 (2)
17 (1) 18 (1) 18 (2) 18 (3) 19 (1) 19 (2) 19 (3) 19 (4)
+++ Search ( 12) = 1
+++ Search ( 18) = 3
+++ Search ( 5) = 4
+++ Search ( 12) = 1
+++ Search ( 6) = 0
+++ Search ( 12) = 1
+++ Search ( 7) = 1
+++ Search ( 17) = 1
+++ Search ( 12) = 1
+++ Search ( 20) = 0
+++ Delete ( 17):
1 (1) 1 (2) 1 (3) 1 (4) 2 (1) 3 (1) 3 (2) 3 (3)
4 (1) 4 (2) 5 (1) 5 (2) 5 (3) 5 (4) 7 (1) 8 (1)
8 (2) 9 (1) 9 (2) 9 (3) 9 (4) 9 (5) 10 (1) 11 (1)
11 (2) 11 (3) 12 (1) 13 (1) 13 (2) 14 (1) 16 (1) 16 (2)
18 (1) 18 (2) 18 (3) 19 (1) 19 (2) 19 (3) 19 (4)
+++ Delete ( 9):
1 (1) 1 (2) 1 (3) 1 (4) 2 (1) 3 (1) 3 (2) 3 (3)
4 (1) 4 (2) 5 (1) 5 (2) 5 (3) 5 (4) 7 (1) 8 (1)
8 (2) 10 (1) 11 (1) 11 (2) 11 (3) 12 (1) 13 (1) 13 (2)
14 (1) 16 (1) 16 (2) 18 (1) 18 (2) 18 (3) 19 (1) 19 (2)
19 (3) 19 (4)
+++ Delete ( 7):
1 (1) 1 (2) 1 (3) 1 (4) 2 (1) 3 (1) 3 (2) 3 (3)
4 (1) 4 (2) 5 (1) 5 (2) 5 (3) 5 (4) 8 (1) 8 (2)
10 (1) 11 (1) 11 (2) 11 (3) 12 (1) 13 (1) 13 (2) 14 (1)
16 (1) 16 (2) 18 (1) 18 (2) 18 (3) 19 (1) 19 (2) 19 (3)
19 (4)
+++ Delete ( 20):
1 (1) 1 (2) 1 (3) 1 (4) 2 (1) 3 (1) 3 (2) 3 (3)
4 (1) 4 (2) 5 (1) 5 (2) 5 (3) 5 (4) 8 (1) 8 (2)
10 (1) 11 (1) 11 (2) 11 (3) 12 (1) 13 (1) 13 (2) 14 (1)
16 (1) 16 (2) 18 (1) 18 (2) 18 (3) 19 (1) 19 (2) 19 (3)
19 (4)
+++ Delete ( 11):
1 (1) 1 (2) 1 (3) 1 (4) 2 (1) 3 (1) 3 (2) 3 (3)
4 (1) 4 (2) 5 (1) 5 (2) 5 (3) 5 (4) 8 (1) 8 (2)
10 (1) 12 (1) 13 (1) 13 (2) 14 (1) 16 (1) 16 (2) 18 (1)
18 (2) 18 (3) 19 (1) 19 (2) 19 (3) 19 (4)
Cleaning up...
Note: Although you do not need to balance the height of BSTs supporting duplicates, think about the difficulties in the process. In the extreme situation when all the n values inserted in T are equal, we get a tree of height n − 1. As per the definition, this tree cannot be height balanced.
In order to make height balancing possible, we require both the left and the right subtrees to contain equal values. We insert in the above way (equal values initially go to the right subtree), but subsequent rotations may bring some equal values to the left subtree. In this case, the BST ordering is the lexicographic ordering on the pair (value,insertion_time). Although insertion times are not explicitly stored in the nodes, this insertion with rotations will respect the lexicographic ordering. But then, how will search and delete behave? Will they still be doable in O(h) time?