Programming Assignment 6
The inorder traversal of a binary search tree (BST) prints the key values in sorted order. In the class, we have seen a recursive function for carrying out the in-order traversal. In this exercise, you implement the in-order traversal of a BST using only a constant amount of extra space. This implies the following.
- Maintain only left and right child pointers in each node. Do not maintain parent pointers.
- The standard recursive function incurs a recursion depth of h(T). Since this is not constant space, you are not allowed to use recursion. Your traversal function should be iterative (a simple while loop).
- Do not use a stack of pointers to emulate recursion, because such a stack will again call for O(h(T)) space.
- The function should run in Θ(n) time for a BST with n nodes.
- Only three pointers and an extra flag indicating the type of the next move suffice.
The idea behind this traversal algorithm is explained in the following figure. The pointer p points to the node which we are currently visiting. The parent of p is pointed to by another pointer q. If p points to the root, then q is NULL. The links from the root to the node pointed to by q are appropriately reversed so that these pointers function as parent pointers.
At any node, four types of movements are possible:
- Down-left: This situation may occur in both the parts of the figure below. If the left subtree of p is not NULL, carry out the down-left movement. This means reversal of another link, that is, the left pointer of p will point to q, and both p and q will move down the tree by one level, and you continue further down-left movement. If the left subtree of p was NULL, print the key at p, and schedule the next movement as a down-right movement.
- Down-right: This situation may occur in both the parts of
the figure below. Now, you are done with the left subtree of p,
and want to explore the right subtree of p. If the right subtree
of p is not NULL, carry out the down-right movement, that is,
adjust the right pointer of p to point to q, move p
and q down the tree by one level, and schedule the next movement
to be a down-left movement. On the other hand, if the right
subtree of p was NULL, then you are done at p. In this
case, compare the keys at p and q to determine whether
the next movement will be up-left (left side of the figure below) or
up-right (right side of the figure).
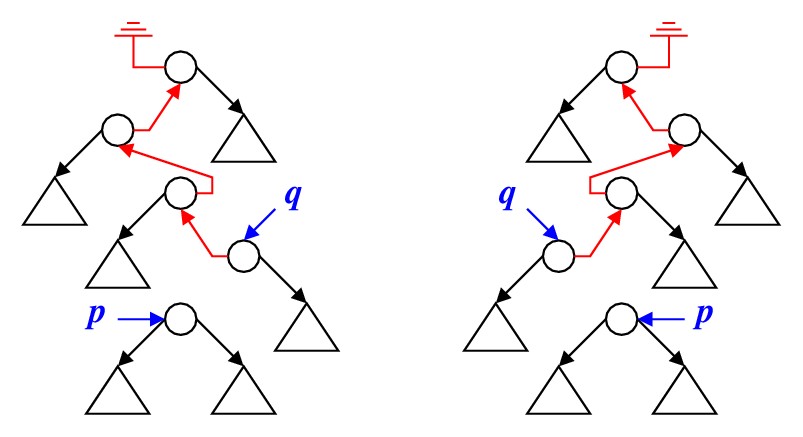
- Up-left: In this case, you have completed visiting the entire subtree rooted at p, and plan to make an upward movement to the node q (see the left side of the above figure). Restore the reversed left link of q, move p and q up the tree by one level, print the key at the new p, and schedule the next movement to be a down-right movement (because the right subtree at the new p is not yet printed).
- Up-right: In this case too, you have completed visiting the entire subtree rooted at p, and plan to make an upward movement to the node q (see the right side of the above figure). This means you are done with the subtree rooted at q. Restore the reversed right link of q, and move p and q one level up the tree. Continue your upward movement, but decide whether the next movement will be up-left (left side of the above figure after the updating of p and q) or up-right (right side of the figure after the update) depending upon the keys at the current nodes p and q.
Write a program to do the following.
- Write the BST insertion function.
- Write the in-order traversal function using the above algorithm.
- Write a function to free the nodes in a BST recursively.
- Write a main() function that creates an initially empty BST, keeps on inserting random integers (may be in the range 1--99) for a certain number of iterations (like 20--30), prints the in-order listing of the tree after each insertion, frees the tree after the insertion loop, and exits.
Sample output
Initializing the tree T = () Inserting 35 T = (35) Inserting 33 T = (33,35) Inserting 58 T = (33,35,58) Inserting 10 T = (10,33,35,58) Inserting 99 T = (10,33,35,58,99) Inserting 73 T = (10,33,35,58,73,99) Inserting 61 T = (10,33,35,58,61,73,99) Inserting 42 T = (10,33,35,42,58,61,73,99) Inserting 6 T = (6,10,33,35,42,58,61,73,99) Inserting 36 T = (6,10,33,35,36,42,58,61,73,99) Inserting 6 T = (6,10,33,35,36,42,58,61,73,99) Inserting 60 T = (6,10,33,35,36,42,58,60,61,73,99) Freeing the tree T = ()