Programming Assignment 4
Study of Connectivities and Diameters of Random Graphs
Gilbert (1959) and Erdös and Rényi (1959,1960) propose several models of random graphs. In this assignment, we study the G(n,p) model of random graphs specified by two parameters -- the number of nodes n, and a probability p in the range [0,1]. A graph (undirected) G = (V,E) of this family has exactly n nodes (vertices), and for each pair of disinct vertices u and v, the (undirected) edge (u,v) is present in the graph with probability p.
Part 1: Generate random graphs
Write a function that, given the parameters n and p, returns a random undirected graph of the family G(n,p). Use an adjacency-list representation of an undirected graph. The following could be a possible representation of such a graph.
typedef int **graph;
A graph data G is allocated memory to point to an array of n int pointers. The array G[u], after proper allocation of memory, is intended to store the count of neighbors of u at the zeroth index, and the neighbor IDs at the indices 1,2,...,G[u][0]. The vertices are numbered 0, 1, ..., n - 1. You may reallocate memory to each G[u] so that the dynamic array pointed to by it contains exactly deg(u) + 1 int cells.
Part 2: Measure connectivity against p
Vary p from 0 to 1 in suitable steps. For each p, do the following. Generate many (say, one hundred) random graphs of the family G(n,p). Using DFS/BFS, check how many of these randomly generated graphs are connected. Report the fractional occurrence of connected graphs in the generated sample.
Part 3: Measure diameter against p
Vary p from 0 to 1 in suitable steps. For each p, do the following. Generate many (say, one hundred) random graphs of the family G(n,p). In fact, you can use the same sample used in Part 2. Using a shortest-path algorithm, compute the diameters of the connected graphs in the sample. Compute and report the average of these diameters against the current value of p.
Note: The distance d(u,v) between two vertices u and v is defined to be the length of a shortest u,v path. The diameter of G (assumed connected) is the maximum of the distances d(u,v) taken over all possible pairs of vertices u and v of G. The diameter of a disconnected graph is taken to be infinity.
Sample output
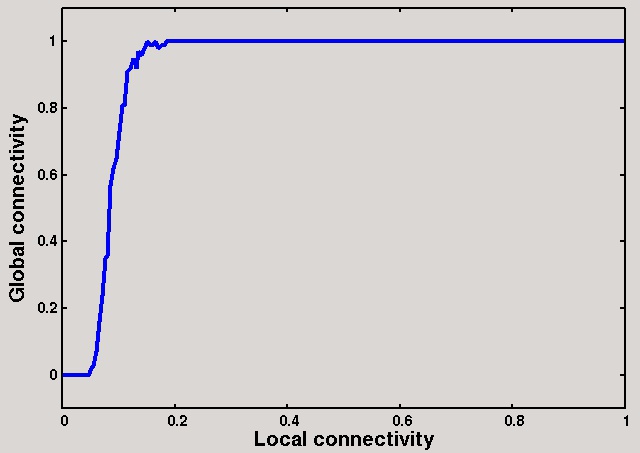
Each line in the following output stores three floating-point values. The first column represents the local connectivity p, the second column represents the global connectivity computed in Part 2, and the third column represents the average diameters of the connected samples as computed in Part 3 (if all the samples are disconnected, a large diameter (infinity) is shown). These results correspond to n = 50.
| Raw output | Plots | Plotting commands (gnuplot) |
|---|---|---|
0.0000 0.00 1000000.0 0.0050 0.00 1000000.0 0.0100 0.00 1000000.0 0.0150 0.00 1000000.0 0.0200 0.00 1000000.0 0.0250 0.00 1000000.0 0.0300 0.00 1000000.0 0.0350 0.00 1000000.0 0.0400 0.00 1000000.0 0.0450 0.00 1000000.0 0.0500 0.02 7.0 0.0550 0.03 7.3 0.0600 0.07 8.1 0.0650 0.16 7.2 0.0700 0.24 6.9 0.0750 0.35 6.2 0.0800 0.36 6.4 0.0850 0.57 5.9 0.0900 0.62 5.6 0.0950 0.65 5.4 0.1000 0.73 5.2 0.1050 0.81 4.9 0.1100 0.81 4.8 0.1150 0.91 4.8 0.1200 0.92 4.4 0.1250 0.95 4.3 0.1300 0.92 4.2 0.1350 0.97 4.2 0.1400 0.96 4.1 0.1450 0.98 4.0 0.1500 1.00 4.0 0.1550 0.99 3.9 0.1600 0.99 3.8 0.1650 1.00 3.7 0.1700 0.98 3.6 0.1750 0.99 3.5 0.1800 0.99 3.3 0.1850 1.00 3.4 0.1900 1.00 3.2 0.1950 1.00 3.1 0.2000 1.00 3.1 0.2050 1.00 3.1 0.2100 1.00 3.0 0.2150 1.00 3.0 0.2200 1.00 3.0 0.2250 1.00 3.0 0.2300 1.00 3.0 0.2350 1.00 3.0 0.2400 1.00 3.0 0.2450 1.00 3.0 0.2500 1.00 3.0 ... 0.9000 1.00 2.0 0.9050 1.00 2.0 0.9100 1.00 2.0 0.9150 1.00 2.0 0.9200 1.00 2.0 0.9250 1.00 2.0 0.9300 1.00 2.0 0.9350 1.00 2.0 0.9400 1.00 2.0 0.9450 1.00 2.0 0.9500 1.00 2.0 0.9550 1.00 2.0 0.9600 1.00 2.0 0.9650 1.00 2.0 0.9700 1.00 2.0 0.9750 1.00 2.0 0.9800 1.00 2.0 0.9850 1.00 2.0 0.9900 1.00 2.0 0.9950 1.00 2.0 1.0000 1.00 1.0 |
|
unset key set xtics font "Freesans,14" set ytics font "Freesans,14" set xlabel "Local connectivity" font "Freesans,20" set ylabel "Global connectivity" font "Freesans,20" set yrange [-0.1:1.1] plot "randgraph.dat" using 1:2 with lines ls 3 lw 4 set xlabel "Local connectivity" font "Freesans,20" set ylabel "Average diameter" font "Freesans,20" set yrange [-0.1:10] plot "randgraph.dat" using 1:3 with lines ls 4 lw 4 |
Your program should work for n = 100.