Assignment 6
The exercise
A graph (more technically, a directed simple graph) G=(V,E) is a set V of vertices (also called nodes) and a set E of edges, where each edge is a pair of distinct vertices. It is customary to draw a graph with vertices indicated by circles and edges represented by directed line segments (or curves) between pairs of vertices. We do not allow an edge to start and end at the same vertex. (Such an edge is called a loop.) We also disallow multiple edges between two vertices. A graph with eight vertices is shown in the following figure:
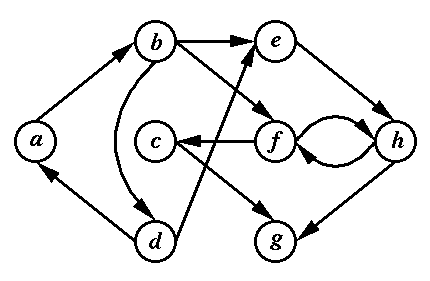
We assume also that each vertex of a graph has a (unique) label (name). In the above figure we have used the letters a through h to label the vertices.
In this exercise one studies two ways of representing graphs.
Adjacency matrix representation
Let G be a graph with n vertices. An adjacency matrix is an nxn matrix with rows and columns labeled by the vertex labels. The (i,j)-th entry in the matrix is 1, if there is an edge from vertex i to vertex j in G. It is 0, otherwise. For example, the adjacency matrix representation of the above graph is as follows:
| a | b | c | d | e | f | g | h | |
|---|---|---|---|---|---|---|---|---|
| a | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| b | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| c | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| d | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| e | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| f | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| g | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| h | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
Linked list representation
In this representation one uses nodes (struct node), each consisting of a label and a pointer to a node of similar type. Let again G be a graph with n vertices. One first creates an array of n nodes to represnt the n vertices of the graph. The pointer at a node heads a linked list of nodes representing the edges from the head node. The linked list representation of the above graph is as shown in the following figure:
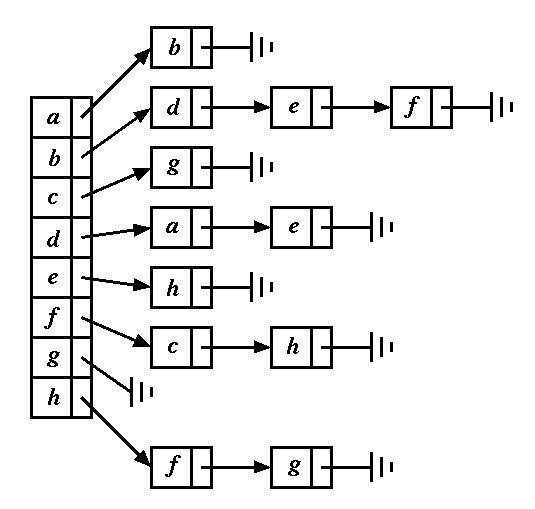
Implement both these representations of a graph using dynamic memory allocation. For example, you may use the following realization of the adjacency matrix:
typedef struct {
int noOfNodes;
char *label;
int **data;
} adjMat;
and the following for nodes in the linked list representation:
struct _node {
char label;
struct _node *next;
};
typedef struct _node node;
Write the following routines:
- A routine to generate the adjacency matrix for a random graph.
- A routine to generate the linked list for a random graph.
- A routine to print an adjacency matrix.
- A routine to print the linked list info.
- A routine that converts the adjacency matrix representation of a graph to the corresponding linked list representation.
- A routine that converts the linked list representation of a graph to the corresponding adjacency matrix representation.
Note that your routines for generating random graphs must avoid loops and multiple edges.
Show the output of your program on (random) graphs with 20 vertices.
Sample output
The following are sample runs for randomly generated graphs with 10 vertices.
Generating random adjacency matrix :
A B C D E F G H I J
A 0 1 0 0 1 0 0 1 1 1
B 0 0 1 1 1 0 1 1 1 0
C 1 1 0 0 0 1 1 1 0 1
D 1 0 1 0 1 1 1 1 1 1
E 1 0 1 1 0 0 0 0 1 1
F 1 1 0 1 0 0 0 1 0 1
G 0 1 1 1 0 1 0 1 1 1
H 0 1 0 0 0 0 1 0 1 0
I 1 1 1 0 0 0 1 0 0 0
J 1 1 0 0 0 1 1 1 1 0
The corresponding linked list :
Label : A. Links to : B E H I J
Label : B. Links to : C D E G H I
Label : C. Links to : A B F G H J
Label : D. Links to : A C E F G H I J
Label : E. Links to : A C D I J
Label : F. Links to : A B D H J
Label : G. Links to : B C D F H I J
Label : H. Links to : B G I
Label : I. Links to : A B C G
Label : J. Links to : A B F G H I
-----------------------------------------------------
Generating random linked list :
Label : a. Links to : b d f i
Label : b. Links to : f g h
Label : c. Links to : b g h j
Label : d. Links to : b c g h
Label : e. Links to : a c d g h j
Label : f. Links to : a c d h
Label : g. Links to : b f h
Label : h. Links to : b d f i j
Label : i. Links to : b d h
Label : j. Links to :
The corresponding adjacency matrix :
a b c d e f g h i j
a 0 1 0 1 0 1 0 0 1 0
b 0 0 0 0 0 1 1 1 0 0
c 0 1 0 0 0 0 1 1 0 1
d 0 1 1 0 0 0 1 1 0 0
e 1 0 1 1 0 0 1 1 0 1
f 1 0 1 1 0 0 0 1 0 0
g 0 1 0 0 0 1 0 1 0 0
h 0 1 0 1 0 1 0 0 1 1
i 0 1 0 1 0 0 0 1 0 0
j 0 0 0 0 0 0 0 0 0 0
-----------------------------------------------------