Assignment 3

---

Exercise 1

Write a function that, given two points (x1,y1) and (x2,y2) in the plane, returns the distance between the points.

Write another function that computes the radius of the circle x²+y²+ax+by+c defined by the triple (a,b,c). Note that for some values of (a,b,c) this radius is not defined. In that case your function should return some negative value.

Ask the user to give two triples (a1,b1,c1) and (a2,b2,c2) so as to define two circles. Use the above two functions to determine which of the following cases occurs:

• One or both of the circles is/are undefined.
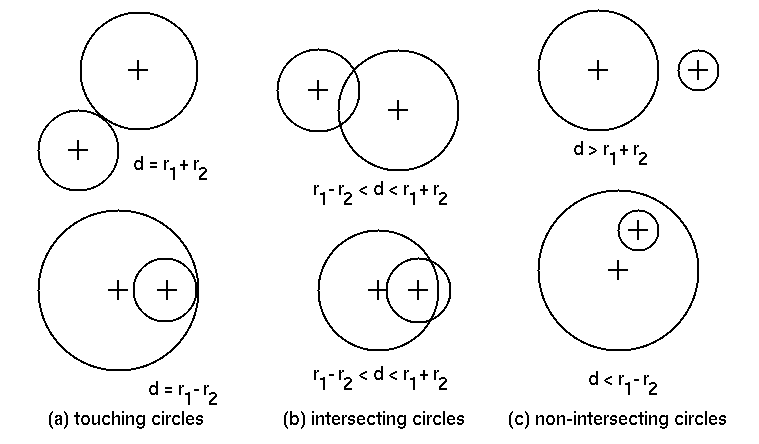
• The two circles touch (i.e., meet at exactly one point).
• The two circles intersect (at two points).
• The two circles do not intersect at all.

The following figure explains the last three possibilities. In the figure d represents the distance between the centers of the two circles, r₁ the radius of the bigger circle and r₂ the radius of the smaller circle.

Sample output

a1 = 0
b1 = 0
c1 = -1
a2 = -3
b2 = 0
c2 = 1
Radius of the first circle = 1.000000
Radius of the second circle = 1.118034
Distance between the centers = 1.500000
The two circles intersect.

a1 = 0
b1 = 0
c1 = -2
a2 = 0
b2 = -10
c2 = 15
Radius of the first circle = 1.414214
Radius of the second circle = 3.162278
Distance between the centers = 5.000000
The two circles do not intersect.

a1 = 6
b1 = -6
c1 = 0
a2 = -8
b2 = 8
c2 = 0
Radius of the first circle = 4.242641
Radius of the second circle = 5.656854
Distance between the centers = 9.899495
The two circles touch.

a1 = 1
b1 = 2
c1 = 3
a2 = 4
b2 = 5
c2 = 6
Radius of the first circle = -1.000000
(a1,b1,c1) does not define a circle.
Radius of the second circle = 2.061553

Test input

Report the output of your program for the following inputs:

a1	b1	c1	a2	b2	c2
1	1	-1	1	1	1
0	2	-3	-2	2	1
2	-2	1	0	0	-9
-4	-4	-2	-4	6	11
-4	-6	13	0	-6	5
-4	-4	4	-10	-4	24
1	-1	0.25	0	-1	-0.75
0.5	-0.5	0.125	0	0	0
0	0	-625	-36	-48	875
0	0	-25	-7.2	-9.6	35

---

Exercise 2

Read two integers n and b from the terminal (with n>=0 and b>1) and express n in base b. For example, the decimal expansion of 345 in base 10 is

345 = 3 x 102 + 4 x 10 + 5.

Note that in this case 5 = 345 % 10 and 34 = 345 / 10; Similarly, the expansion of 345 in base 16 is

6789 = 1 x 163 + 10 x 162 + 8 x 16 + 5 = (1,10,8,5)16.

Here 5 = 6789 % 16 and 424 = 6789 / 16 = (1,10,8)₁₆.

Write a recursive function that makes this base conversion.

Sample output

n = 345
b = 10
(345)_10 = (3,4,5)_10

n = 345
b = 16
(345678)_10 = (1,5,9)_16

n = 987654321
b = 123
(987654321)_10 = (4,38,92,23,114)_123

Test input

Report your output for the following input values:

n	b
0	12
34	56
78	78
9801	99
15626	25
65535	8
536870911	2
536870912	16
1111111111	11
1273412531	47

---

Lab home