Theorem: If we remove a square from a 2^kx2^k chessboard, the remaining part of the board can be covered completely by non-overlapping L-shaped objects. Here an L-shaped object consists of three squares. Four types of L-shaped objects are given in the figure below.

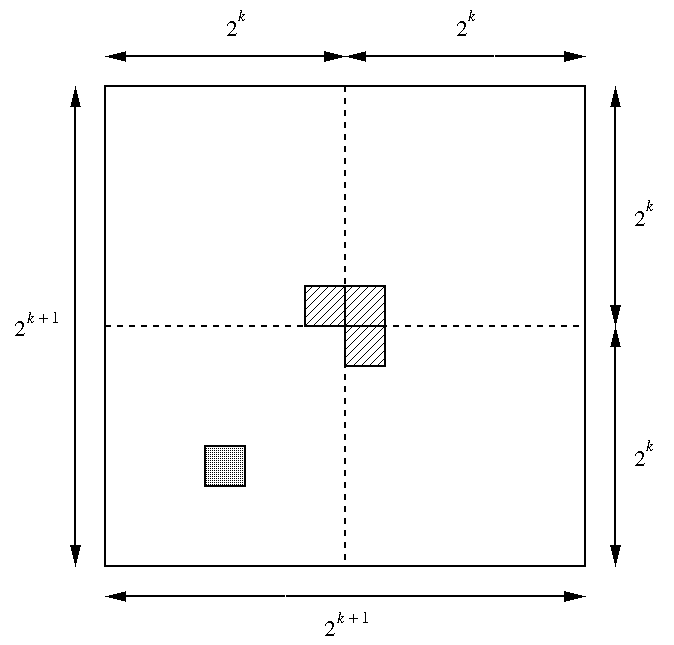
Proof. We proceed by induction on k. For k=1 the theorem is obvious. So assume that the result holds for some value of k>=1 and we are given a 2^k+1x2^k+1 chessboard and a square in it. (See the figure below.) We first divide the board in four equal parts, each of size 2^kx2^k. Assume that the given square is in the lower left part. Remove three squares from the three other parts as shown in the figure. By induction each part can now be covered by L-shaped objects. Finally, add an L-shaped object covering the three squares removed near the center. QED

In this assignment you are supposed to compute an explicit covering of a 2^kx2^k board minus a square. Write a recursive procedure based on the idea given in the proof above. Make only two recursive calls for each value of k>1. Since the three parts with squares removed from the corners are identical in configuration (but differ only in orientation), a single recursive call suffices for these three parts.

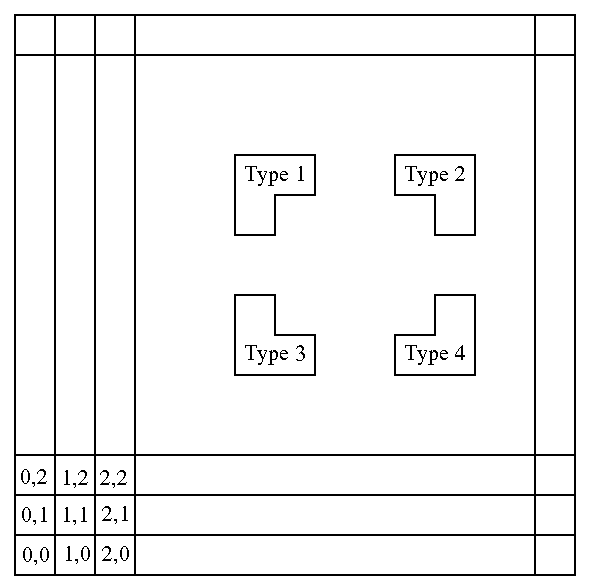
The squares in the board are numbered as described in the next figure. The numbering starts from zero at the lower left corner in both horizontal and vertical directions. Four types of L-shaped objects are also shown. An L-shaped object is identified by the number (i,j) of its central square and its type (an integer between 1 and 4).

Output

For viewing the covering generated by your code, generate a PostScript file. You don't have to learn how to write PostScript files. Follow the instructions given below. Suppose that you want to generate the output file chess.ps.

• Copy the file preamble.ps to chess.ps.

• Append the line

  dim D
  

  Here dim is the (x or y) dimension of the chessboard (2^k).

• Then for each L-shaped object generated by your code, add the line

  i j LT
  

  Here (i,j) are the row and column numbers of the central cell of the L-shaped object and T is the type of the L-shaped object. Follow the convention described in the figure above.

• Let the initial square removed have the number (x,y). Add the line

  x y H
  

  to chess.ps.

• Finally add the line

  showpage
  

  at the end of the output file.

chess.ps is now a complete PostScript file that can be viewed or printed.

An example for the case k=3 (the standard chessboard) is given below. The (4,6)-th square is initially removed. Your program should generate something like the following lines:

8 D
0 7 L1
3 7 L2
0 4 L3
2 5 L1
1 6 L1
5 7 L2
7 7 L2
4 4 L3
7 4 L4
6 5 L4
0 3 L1
2 2 L3
0 0 L3
3 0 L4
1 1 L3
5 2 L4
7 3 L2
4 0 L3
7 0 L4
6 1 L4
3 3 L3
4 6 H
showpage

Submit the following files:

• The source code (chess.c).
• The output PostScript file for k=5 or 6 (chess.ps).

   srand((unsigned int)wxyz);

Home