3D Segmentation
by Slice-based Vertex-weighted Reeb GraphAlgorithm
N. Karmakar, A. Biswas, and P. Bhowmick,Segmentation of 3D Object Articulations by Slice-based Vertex-weighted Reeb Graph,
18th IAPR International Conference on Discrete Geometry for Computer Imagery: DGCI'14, 10-12 September 2014, Siena, Italy, LNCS 8668, pp. 370-383.
Contribution
We have proposed a fast and efficient algorithm for segmentation of the articulated components of 3D objects. The algorithm is marked by several novel features, such as DCEL-based orthogonal slicing, weighted Reeb graph with slice area as vertex weight, and graph cut by exponential averaging. Each of the three sets of orthogonal slices obtained from the object along three coordinate planes is represented by a vertex-weighted Reeb graph of low complexity, since the slicing is done in a grid of an appropriate resolution. The linear subgraphs in a Reeb graph are traversed starting from its leaf node up to an articulation node or a node whose weight exceeds a certain threshold. The threshold value is set dynamically, based on exponential averaging of the predecessor weights in the concerned subgraph. The nodes visited in each linear subgraph are marked by a unique component number, which helps in doing the inverse mapping to mark the articulated regions of the 3D object, resulting in final segmentation. Theoretical analysis shows that the algorithm runs faster for objects with smaller surface area and for larger grid resolutions. The algorithm is stable, efficient, invariant to rotation, and leads to natural segmentation, as evidenced by experimentation.Total time complexity
$O(n_f\log n_f)=O(\alpha/g^2\log(\alpha/g^2))$, where $n_f=\,$number of UGC-faces on the object surface, $\alpha=\,$surface area of the 3D object, and $g=\,$grid size.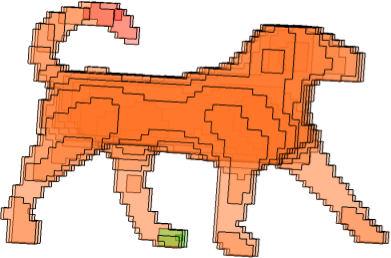 yz-slices |
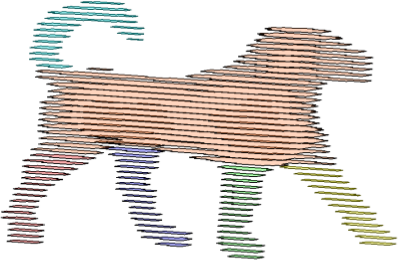 zx-slices |
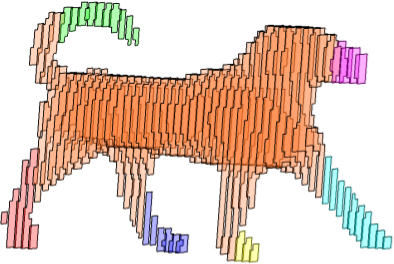 xy-slices |
 final segmentation |
| Figure: Results on Dog object (g = 2). Slices parallel to yz-, zx-, xy-plane, with segments marked in different colors, and the final articulated portions with the central region. | |












